Question

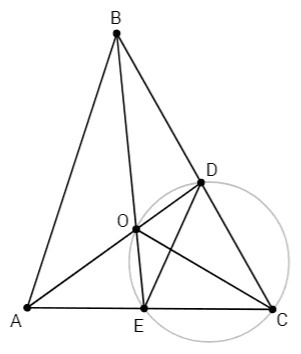
В треугольнике АВС проведены биссектрисы AD и ВЕ, пересекающиеся в точке О. Известно, что отрезок ОЕ имеет длину, равную 1, а вершина С лежит на окружности, проходящей через точки Е, D, О. Найдите стороны и углы треугольника ЕDO.

Пожалуйста, подробное решение.

Answer 1

Вписанные углы, опирающиеся на одну дугу, равны.
∠OCD=∠OED, ∠OCE=∠ODE

Биссектрисы внутренних углов треугольника пересекаются в одной точке.
CO - биссектриса ∠С, ∠OCD=∠OCE

∠OED=∠ODE
△ODE - равнобедренный, OD=OE=1

Равные вписанные углы опираются на равные дуги.
∪OE=∪OD

Вписанный угол равен половине дуги, на которую опирается.
∠C= ∪ED/2 = (∪OE+∪OD)/2 =∪OD

Угол между двумя касательными из одной точки равен полуразности большей и меньшей высекаемых дуг.
∠A/2= (∪DC -∪OE)/2
∠B/2= (∪EC -∪OD)/2

∠A+∠B+∠C=180 <=>
∪DC -∪OE +∪EC -∪OD +∪OD =180 <=>
∪DC +∪EC -∪OE =180

∪DC +∪EC +∪OE +∪OD =360

∪OE +∪OD +∪OE =360-180 <=> 3∪OE =180 <=> ∪OE=60

∠OED=∠ODE=∪OE/2 =30
∠DOE= 180-30*2 =120

ED= √(OD^2 +OE^2 -2OD*OE*cos120) = √(2 +2/2) =√3