Question

В трапеции проведены два отрезка, параллельных основанию и соединяющих боковые стороны. один из них равный√ 7, делит трапецию на две подобные трапеции, а другой равный 5 делит трапецию на две трапеции, равные по площади. найдите отношение отрезков на которые делит боковую сторону данные отрезки.

Answer 1

Отрезок, разбивающий трапецию на подобные трапеции, равен среднему геометрическому оснований.
√7= √(ab)

Отрезок, разбивающий трапецию на равновеликие трапеции, равен среднему квадратичному оснований.
5= √[(a^2 +b^2)/2]

{ab=7 <=> b=7/a
{a^2 +b^2=50 <=> a^2 +49/a^2 =50 <=> (a^2)^2 -50a^2 +49 =0
a=7; b=1

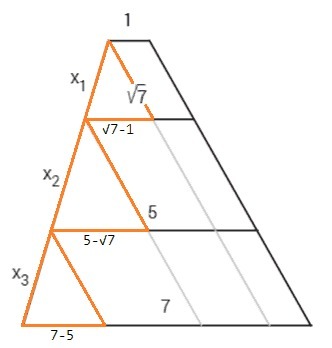
Прямые, параллельные боковой стороне трапеции, и данные отрезки отсекают подобные треугольники со сторонами (x1, √7-1); (x2, 5-√7); (x3, 2).

Ответ: x1 : x2 : x3 = (√7-1) : (5-√7) : 2