Предмет: Геометрия,
автор: MiamiKing
Привет решите пожалуйста!!
Спасибо
Приложения:
Ответы
Автор ответа:
0
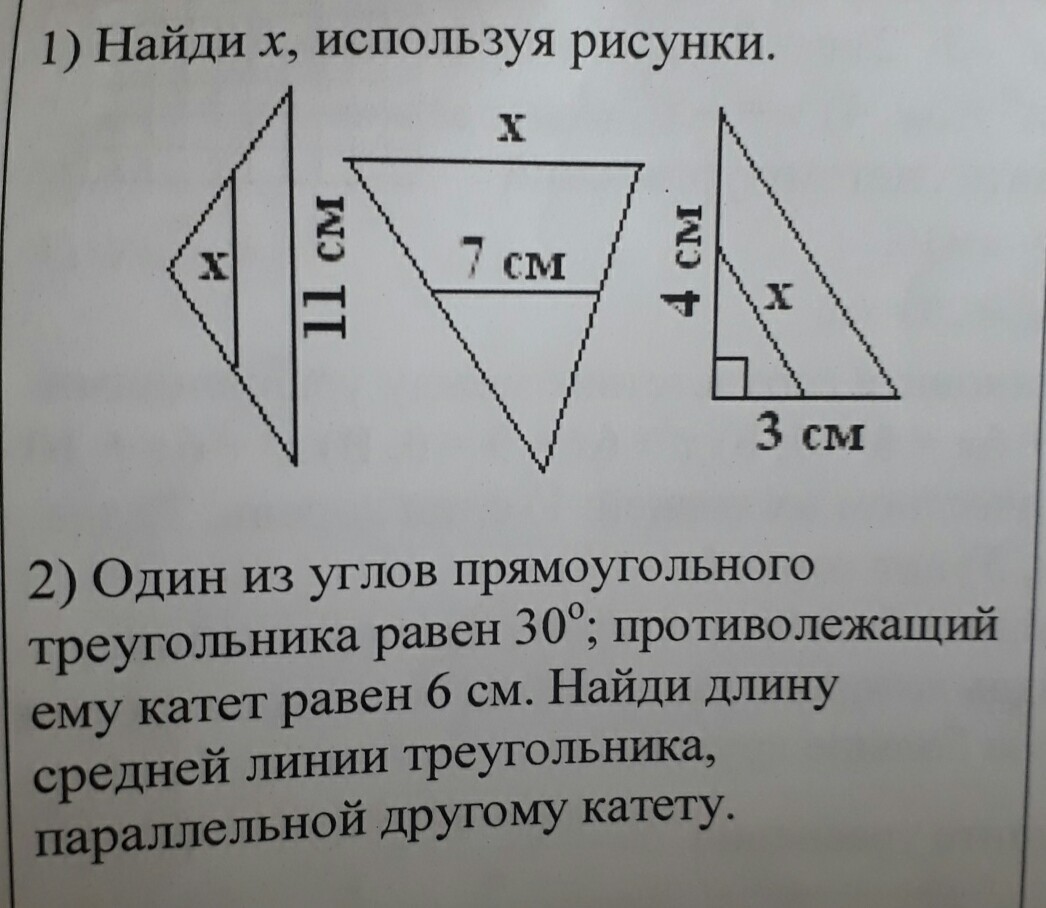
1) По теореме средняя линия треугольника параллельна одной из его сторон и равна её половине.
В первом случае x=11см/2=5,5см.
Во втором случае x=7см•2=14см
В третьем случае сначала надо найти третью сторону треугольника. Так как треугольник прямоугольный, то можно воспользоваться теоремой Пифагора( Квадрат гипотенузы равен сумме квадратов катетов). То есть нам нужно найти гипотенузы( сторону, лежащую против прямого угла). Она будет равна корню квадратному из 16+9, то есть из 25. Следовательно, гипотенузы равна 5. Теперь найдём х. х-это средняя линия треугольника. х= 5см/2=2,5см.
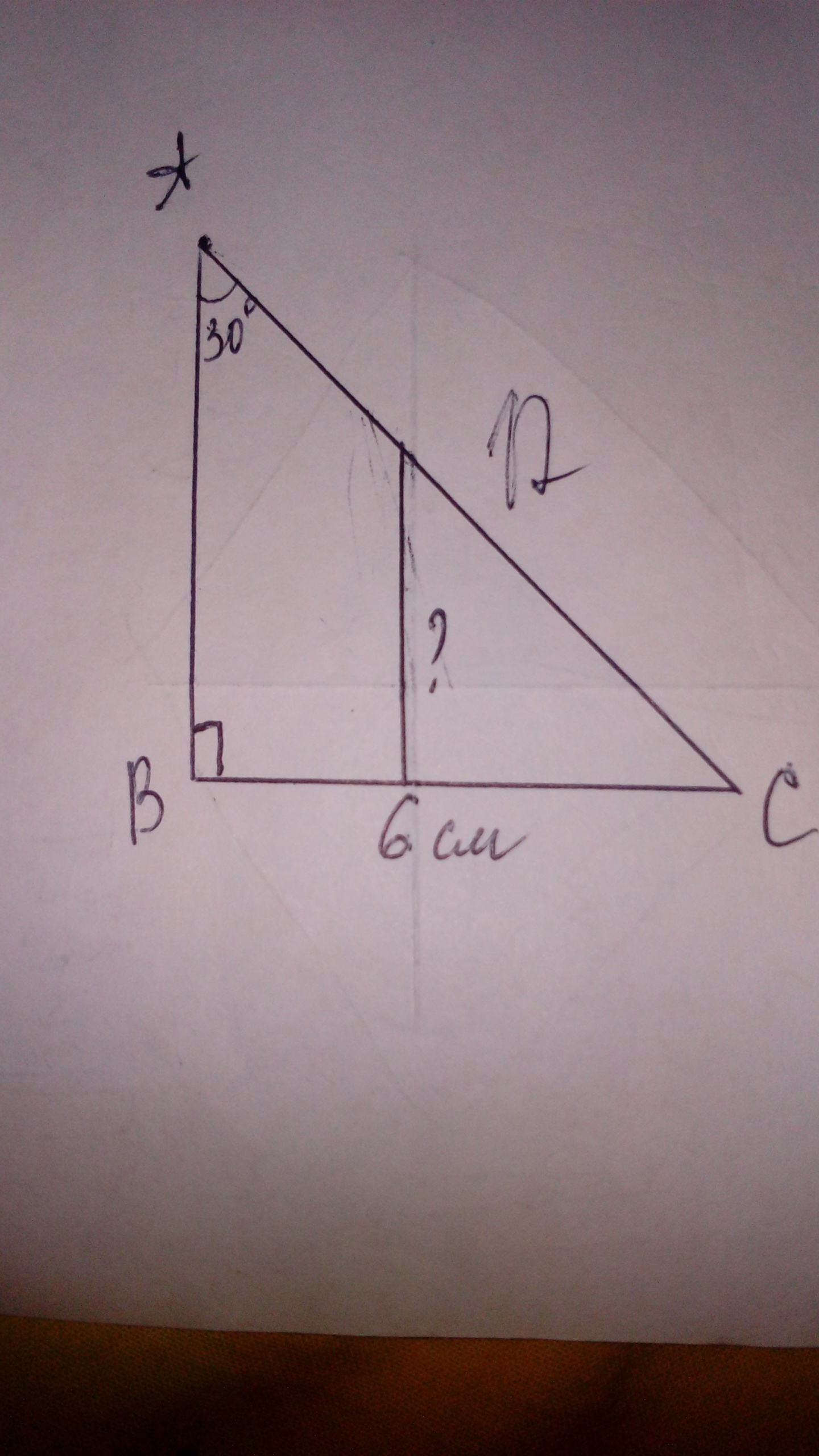
2) Имеем дело с прямоугольным треугольником. Вспомним теорему: "В прямоугольном треугольнике катет, лежащий против угла в 30 градусов, равен половине гипотенузы. Следовательно, мы можем найти гипотенузу: 6см•2=12 см. По теореме Пифагора имеем: другой катет= корню квадратному из 108= 2 корням из 27. Средняя линия будет равна корню из 27.
В первом случае x=11см/2=5,5см.
Во втором случае x=7см•2=14см
В третьем случае сначала надо найти третью сторону треугольника. Так как треугольник прямоугольный, то можно воспользоваться теоремой Пифагора( Квадрат гипотенузы равен сумме квадратов катетов). То есть нам нужно найти гипотенузы( сторону, лежащую против прямого угла). Она будет равна корню квадратному из 16+9, то есть из 25. Следовательно, гипотенузы равна 5. Теперь найдём х. х-это средняя линия треугольника. х= 5см/2=2,5см.
2) Имеем дело с прямоугольным треугольником. Вспомним теорему: "В прямоугольном треугольнике катет, лежащий против угла в 30 градусов, равен половине гипотенузы. Следовательно, мы можем найти гипотенузу: 6см•2=12 см. По теореме Пифагора имеем: другой катет= корню квадратному из 108= 2 корням из 27. Средняя линия будет равна корню из 27.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: cernovas194
Предмет: Математика,
автор: lilpup0999
Предмет: Алгебра,
автор: mariakasiyan
Предмет: Информатика,
автор: valyaevaolga
Предмет: Алгебра,
автор: BlackMedic