Предмет: Алгебра,
автор: 545tyuyuyu
Помогите пожалуйста с уравнением :с
Приложения:
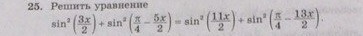
Ответы
Автор ответа:
0
Понизим степень по формуле sin²x=(1-cos2x)/2
(1-cos3x)/2+(1-cos(π/2-5x))/2=(1-cos11x)/2+(1-cos(π/2-13x))/2
1-cos3x+1-sin5x=1-cos11x+1-sin13x
sin13x-sin5x+cos11x-cos3x=0
2sin4xcos9x-2sin4xsin7x=0
2sin4x*(cos9x-sin7x)=0
sin4x=0⇒4x=πk⇒x=πk/4,k∈z
cos9x-sin7x=0
cos9x-cos(π/2-7x)=0
-2sin(8x-π/4)sin(x+π/4)=0
sin(8x-π/4)=0⇒8x-π/4=πk⇒8x=π/4+πk⇒x=π/32+πk/8,k∈z
sin(x+π/4)=0⇒x+π/4=πk⇒x=-π/4+πk,k∈z
(1-cos3x)/2+(1-cos(π/2-5x))/2=(1-cos11x)/2+(1-cos(π/2-13x))/2
1-cos3x+1-sin5x=1-cos11x+1-sin13x
sin13x-sin5x+cos11x-cos3x=0
2sin4xcos9x-2sin4xsin7x=0
2sin4x*(cos9x-sin7x)=0
sin4x=0⇒4x=πk⇒x=πk/4,k∈z
cos9x-sin7x=0
cos9x-cos(π/2-7x)=0
-2sin(8x-π/4)sin(x+π/4)=0
sin(8x-π/4)=0⇒8x-π/4=πk⇒8x=π/4+πk⇒x=π/32+πk/8,k∈z
sin(x+π/4)=0⇒x+π/4=πk⇒x=-π/4+πk,k∈z
Похожие вопросы