Предмет: Алгебра,
автор: hoganjohnson007
Ребята помогите с 8 12 19 номерами!!!! ПОЖАЛУЙСТА Тема биквадратные уравнения
Приложения:

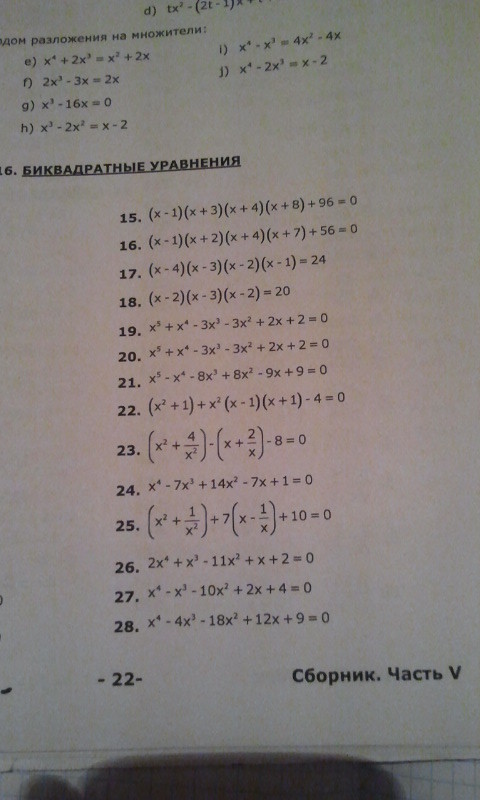
Ответы
Автор ответа:
0
ну что мы здесь делаем, приводим к стандартному виду
8.

замена:


по теореме Виета:



обратная замена:










12. вот лично я в таких случаях люблю использовать метод Горнера (ладно, я вообще очень люблю применять его, когда речь заходит об уравнениях высших степеней)
раскрыв скобки, имеем






 - корней нет
- корней нет
19. снова метод Горнера (с его сутью подробно можно ознакомиться на многих веб-ресурсах)









8.
замена:
по теореме Виета:
обратная замена:
12. вот лично я в таких случаях люблю использовать метод Горнера (ладно, я вообще очень люблю применять его, когда речь заходит об уравнениях высших степеней)
раскрыв скобки, имеем
19. снова метод Горнера (с его сутью подробно можно ознакомиться на многих веб-ресурсах)
Автор ответа:
0
drwndможешь еще решить
Автор ответа:
0
что?
Автор ответа:
0
я щас добавлю
Автор ответа:
0
18 И 24
Похожие вопросы
Предмет: История,
автор: ryslancvuctyn
Предмет: Алгебра,
автор: Aaaaaythpvlduf
Предмет: Немецкий язык,
автор: 6yxoi2
Предмет: Информатика,
автор: Cvetochek005
Предмет: Биология,
автор: mastykovalina