Предмет: Геометрия,
автор: Знания
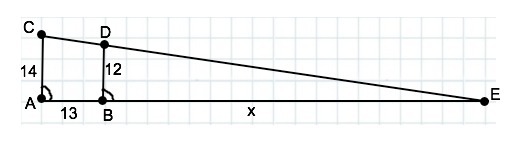
Параллельные прямые AC и BD пересекают плоскость α в точках A и B. Точки C и D лежат по одну сторону от плоскости α. AC=14 см, BD=12 см, AB=13 см.
Докажите, что прямая CD пересекает плоскость α в некоторой точке E. Вычислите длину отрезка AE.
Ответы
Автор ответа:
0
Отрезки параллельных прямых, заключенные между плоскостью и параллельной ей прямой, равны.
АС параллельна ВD, но не равна ей, следовательно, СЕ не параллельна плоскости α и пересекает ее в некоторой т.Е.
АС║BD ⇒ лежат в одной плоскости; т. Е принадлежит прямой CD и лежит в той же плоскости.
В ∆ АСЕ точка B принадлежит АЕ, точка D принадлежит СЕ, BD|║АС по условию, ⇒ треугольники АСЕ и BDE подобны.
Из подобия следует отношение:
АС:BD=АЕ:ВЕ.
Примем длину ВЕ=х
14:12=(13+х):х.
14 х=156+12 х⇒
х=78
АЕ=13+78=91 см
Приложения:
Похожие вопросы
Предмет: Право,
автор: mihaleva1911
Предмет: Литература,
автор: likeass4
Предмет: Алгебра,
автор: wakeupperr22855
Предмет: Математика,
автор: alexbuuu00