Предмет: Алгебра,
автор: taiskorotina
14. Освободите выражение от иррациональности в знаменателе.
а) √(y+1)
б)2√(y+1)
в)√(y+1)/y+1
г)√(y+1)/y+2
Приложения:
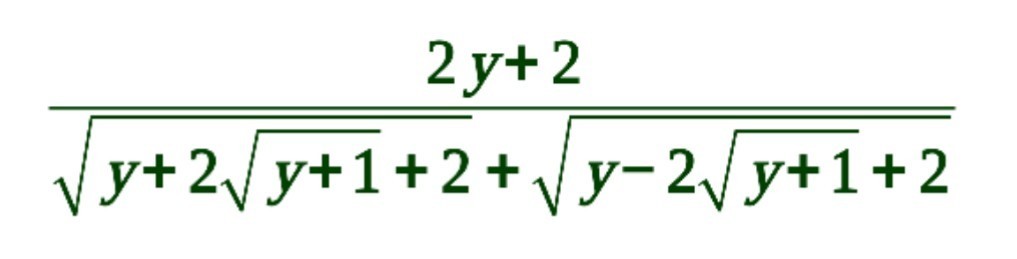
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Физика,
автор: faina12345
Предмет: Другие предметы,
автор: Аноним
Предмет: Физика,
автор: stokakira22
Предмет: Литература,
автор: Rusland5