Question

Правильный многоугольник имеет две оси симметрии, пересекающиеся под углом 30 градусов. Какое наименьшее число сторон может иметь этот многоугольник?

Answer 1

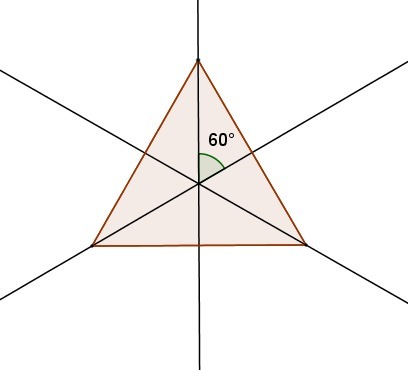
1) Равносторонний треугольник имеет 3 оси  симметрии, каждая проходит через вершину и середину противоположной стороны, угол между любыми двумя осями 60°
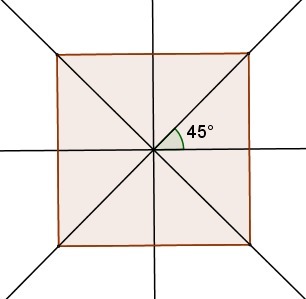
2) Квадрат имеет 4 оси симметрии, каждая проходит либо через противоположные вершины либо через середины противоположных сторон, и угол между любыми двумя осями не меньше 45°.
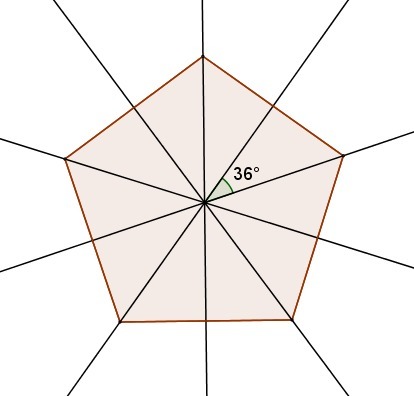
3) Правильный 5-угольник имеет 5 осей симметрии, каждая проходит через вершину и середину противоположной стороны и угол между ними не меньше 36°.
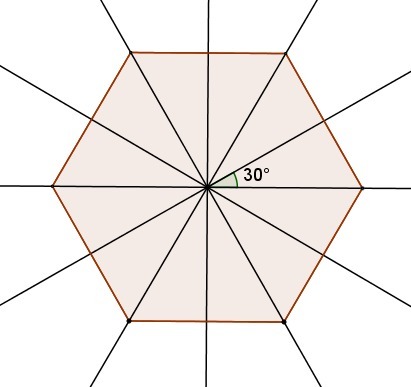
4) Правильный 6-угольник имеет 6 осей симметрии, каждая проходит либо через противоположные вершины либо через середины противоположных сторон, и угол между двумя соседними осями 30°.
Значит, правильный многоугольник с наименьшим числом сторон и углом 30° между осями - правильный 6-угольник.