Question

Противолежащая основанию вершина равнобедренного треугольника удалена от точки пересечения медиан на 32/3, а от точки пересечения серединных перпендикуляров – на 25/2. Вычислите площадь треугольника.

Answer 1

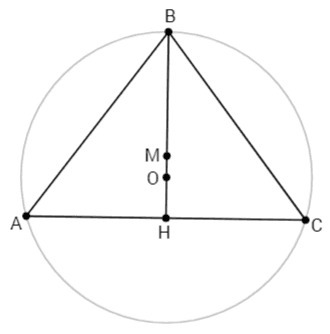
BM=32/3
BO=25/2
AB=BC

Медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины.
BM= 2BH/3 <=> BH= 3BM/2 = 3*32/2*3 =16

В равнобедренном треугольнике медиана к основанию является биссектрисой и высотой.
S= AC*BH/2 =8AC

Точка пересечения серединных перпендикуляров треугольника - центр описанной окружности. BO - радиус описанной окружности.
BO= AB*BC*AC/4S <=>
AB^2= BO*4S/AC = BO*4*8AC/AC =32BO <=>
AB= √(32*25/2) =20

AH= √(AB^2 -BH^2) = √(20^2 -16^2) =12

AC= 2AH = 2*12 =24

S= 8AC = 8*24 =192