Предмет: Алгебра,
автор: irinakellerdal
Помогите решить систему уравнений
Приложения:
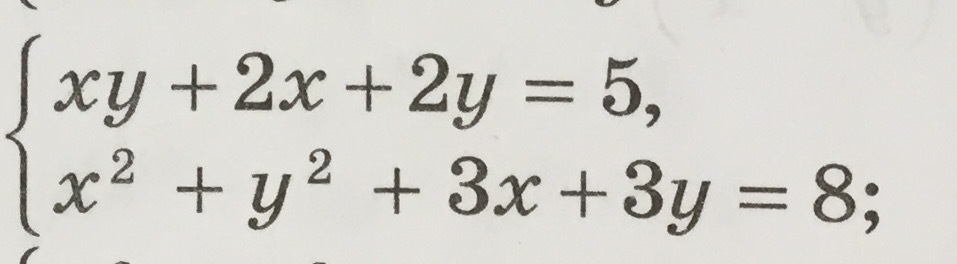
Ответы
Автор ответа:
0
Отсюда
Вернемся к переменным х и у:
1)
Второе уравнение системы не имеет решений (дискриминант отрицательный), поэтому у системы нет решений.
2)
Ответ: (1; 1).
Приложения:

Похожие вопросы
Предмет: Математика,
автор: Lianakka
Предмет: Литература,
автор: Аноним
Предмет: Алгебра,
автор: kaapkalievaaruzan
Предмет: Математика,
автор: хсофик
Предмет: Математика,
автор: ашод