Предмет: Алгебра,
автор: bertain
100 баллов + лучший ответ! При каком наибольшем целом значении параметра а система уравнений имеет два решения? (с подробным решением)
Приложения:
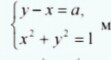
Ответы
Автор ответа:
0
Из первого уравнения выразим у, т.е.  и подставим во второе уравнение
и подставим во второе уравнение

D>0 - уравнение имеет 2 корня, т.е. или
или  откуда
откуда 
Наибольшее значение а=1.
D>0 - уравнение имеет 2 корня, т.е.
Наибольшее значение а=1.
Автор ответа:
0
то же самое но на пальцах
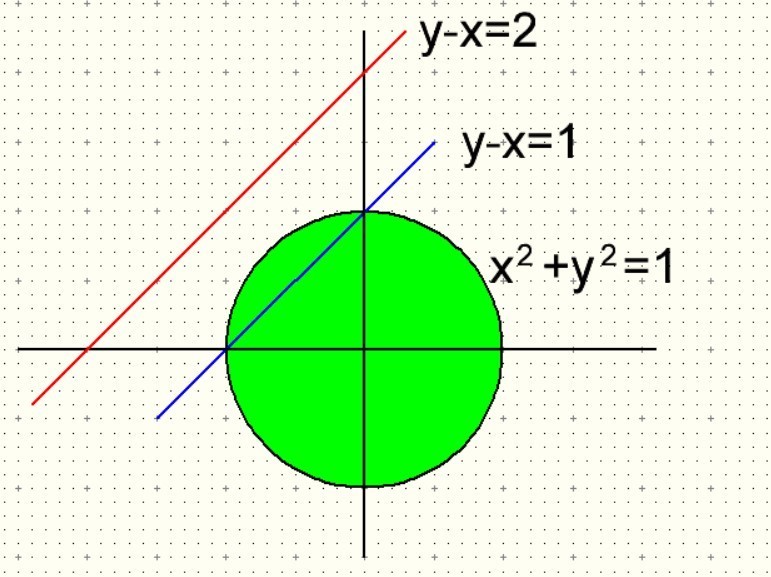
второе уравнение - окружность с центром в начале координат, радиусом 1
первое уравнение - прямая под углом 45 градусов, смещенная относительно начала координат вверх на "а"
очевидно что такая прямая может иметь общие точки с окружностью в диапазоне от минус до плюс корень из двух. причем в названных точках только одно решение.
наибольшее целое значение параметра а при котором именно две точки пересечения это а=1
второе уравнение - окружность с центром в начале координат, радиусом 1
первое уравнение - прямая под углом 45 градусов, смещенная относительно начала координат вверх на "а"
очевидно что такая прямая может иметь общие точки с окружностью в диапазоне от минус до плюс корень из двух. причем в названных точках только одно решение.
наибольшее целое значение параметра а при котором именно две точки пересечения это а=1
Приложения:
Похожие вопросы
Предмет: Французский язык,
автор: voyakinalina
Предмет: Музыка,
автор: tynkasovdaniil
Предмет: Геометрия,
автор: arinakireeva61
Предмет: Математика,
автор: 54365436
Предмет: География,
автор: li8aENTAf7kmrj