Предмет: Геометрия,
автор: ZviNK
Точки соприкосновения вписаного круга делит гипотенузу прямоугольного треугольника на отрезки, один с которых на 14см больше за другой. Найдите площадь треугольника, если радиус вписаного круга = 4см
Ответы
Автор ответа:
1
Радиус окружности, проведенный в точку касания, перпендикулярен касательной.
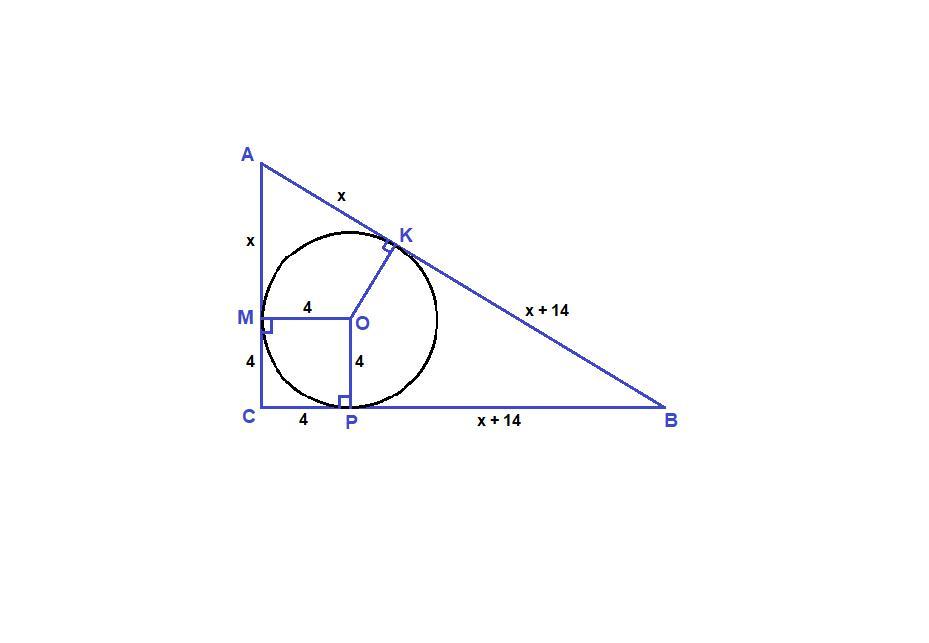
Значит ОК⊥АВ, ОМ⊥АС и ОР⊥ВС.
Отрезки касательных, проведенных из одной точки, равны. Обозначим один отрезок гипотенузы х, а другой х + 14. Тогда
АК = АМ = х
ВК = ВР = х + 14
СМОР - квадрат, СМ = СР = 4.
Составим уравнение по теореме Пифагора:
АВ² = АС² + ВС²
(x + (x + 14))² = (x + 4)² + (4 + x + 14)²
(2x + 14)² = (x + 4)² + (x + 18)²
4x² + 56x + 196 = x² + 8x + 16 + x² + 36x + 324
2x² + 12x - 144 = 0
x² + 6x - 72 = 0
x = 6 или х = - 12 - не подходит по смыслу задачи.
АС = 6 + 4 = 10 см
ВС = 4 + 6 + 14 = 24 см
Sabc = 1/2 AC · BC = 1/2 · 10 · 24 = 120 см²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kreyzifroq
Предмет: Немецкий язык,
автор: kirsall
Предмет: Математика,
автор: alisa3638
Предмет: История,
автор: asddsa27
Предмет: Алгебра,
автор: rakod2