Предмет: Алгебра,
автор: negan72
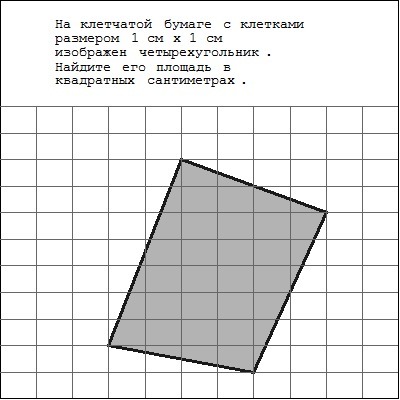
всем привет. столкнулся с такой задачкой пожалуйста помогите и объясните, как ее решать
Приложения:
Ответы
Автор ответа:
0
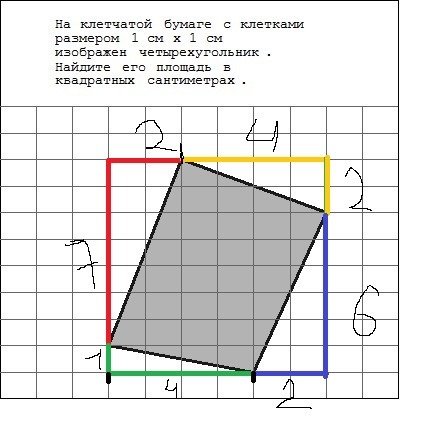
Решать можно нессколькими способами, рассмотрим наиболее простой,
на мой взгляд, в данной ситуации. Достроим исходную фигуру до
прямоугольника с помощью прямоугольных треугольников и вычтем из площади
прямоугольника площади треугольников ( СМ. РИС.)0) Площадь прямоугольника S=8*6=48.
1) Площадь красного п/у Δ s=2*7*1/2=7
2) Площадь оранж. п/у Δ s= 4*2*1/2=4
3)Площадь син. п/у Δ s=6*2*1/2=6
4)Площадь зел. п/у Δ s=4*1*1/2=2
5) Площадь искомой фигуры равна s=48-(7+4+6+2)=29 см^2
1) Площадь красного п/у Δ s=2*7*1/2=7
2) Площадь оранж. п/у Δ s= 4*2*1/2=4
3)Площадь син. п/у Δ s=6*2*1/2=6
4)Площадь зел. п/у Δ s=4*1*1/2=2
5) Площадь искомой фигуры равна s=48-(7+4+6+2)=29 см^2
Приложения:
Автор ответа:
0
Извините, почему-то текст не отформатировался и слился в одну кучу без переносов строк..
Автор ответа:
0
По формуле Пика было бы проще.
Автор ответа:
0
Согласен, для кого-то может и проще, но человек незнакомый мог непонять/запутаться/забыть в дальнейшем
Автор ответа:
0
Согласен.
Автор ответа:
0
Решаем эту задачу по теореме Пика:
S=n+(m/2)-1, где
S - площадь многоугольника,
n - число узлов (пересечения клеток), лежащих внутри многоугольника. Их 33,
m - число узлов (пересечения клеток), лежащих на границах многоугольника (на вершинах и сторонах). Их 6. ⇒
S=33-(6/2)-1=33-3-1=29 (cм²).
Ответ: S=29 см².
S=n+(m/2)-1, где
S - площадь многоугольника,
n - число узлов (пересечения клеток), лежащих внутри многоугольника. Их 33,
m - число узлов (пересечения клеток), лежащих на границах многоугольника (на вершинах и сторонах). Их 6. ⇒
S=33-(6/2)-1=33-3-1=29 (cм²).
Ответ: S=29 см².
Приложения:

Автор ответа:
0
неточность в ответе... n=27 S=27+3-1=29
Автор ответа:
0
потому и абсолютно согласна с Newton1337: с треугольниками сложнее ошибиться))
Автор ответа:
0
Это не неточность, это конкретная ошибка
Автор ответа:
0
Откуда верный ответ мне не ясно
Автор ответа:
0
Очень просто. Я сначала решил с треугольниками. Потом попробовал решить по теореме Пика и ошибся. Я насчитал 33 пересечения. Вывод: предпочтительней решать такие задачи с треугольниками.
Похожие вопросы
Предмет: Алгебра,
автор: likaskat0640
Предмет: Геометрия,
автор: nzhbekbaub
Предмет: Русский язык,
автор: oblomkov05
Предмет: Математика,
автор: alexis27