Предмет: Математика,
автор: GiiR
В задание исследовать данные функции методами дифференциального исчисления и построить их графику. Исследование функции рекомендуется проводить по следующей схеме:
1) Найти область определения функции;
2) Исследовать функцию на непрерывность;
3) Определить, является ли данная функция четной, нечетной;
4) Найти интервалы возрастания и убывания функции и точки ее экстремума;
5) Найти интервалы выпуклости и вогнутости и точки перегиба графика функции;
6) Найти асимптоты графика функции.
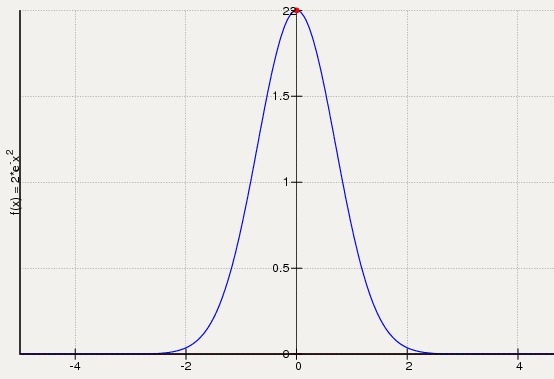
y=2e⁻ˣ²
Ответы
Автор ответа:
0
График функции в приложении.
ДАНО

ИССЛЕДОВАНИЕ
1. Область определения - x∈(-∞;+∞) - непрерывная, разрывов нет.
2.Пересечение с осью Х - х ∈∅ - нет
3. Пересечение с осью У - у(0) =2 при х = 0.
4. Поведение на бесконечности.
lim Y(-∞)=0
lim Y(+∞)=0.
5. Наклонная асимптота - У =0.
6. Проверка на четность.
Y(-x) = Y(x) - функция четная - симметричная относительно оси У.
7. Производная функции

8. Точка экстремума
х = 0.
Значение максимума - Y(0)=2.
9. Возрастает - Х∈(-∞;0)
Убывает - Х∈(0;+∞)
10. Вторая производная

ДАНО
ИССЛЕДОВАНИЕ
1. Область определения - x∈(-∞;+∞) - непрерывная, разрывов нет.
2.Пересечение с осью Х - х ∈∅ - нет
3. Пересечение с осью У - у(0) =2 при х = 0.
4. Поведение на бесконечности.
lim Y(-∞)=0
lim Y(+∞)=0.
5. Наклонная асимптота - У =0.
6. Проверка на четность.
Y(-x) = Y(x) - функция четная - симметричная относительно оси У.
7. Производная функции
8. Точка экстремума
х = 0.
Значение максимума - Y(0)=2.
9. Возрастает - Х∈(-∞;0)
Убывает - Х∈(0;+∞)
10. Вторая производная
Приложения:
Автор ответа:
0
Осталось найти корни второй производной и точки перегиба.
Автор ответа:
0
Надо думать, что это при Х=+/- 1.
Автор ответа:
0
Добрый день!
Автор ответа:
0
Я полагаю, что это полное решение задачи?
Похожие вопросы
Предмет: Математика,
автор: arsik38
Предмет: История,
автор: uliana7007
Предмет: Математика,
автор: oksana153025
Предмет: Математика,
автор: verunyayunitsk