Предмет: Математика,
автор: aurum991
помогите решить ....
Приложения:
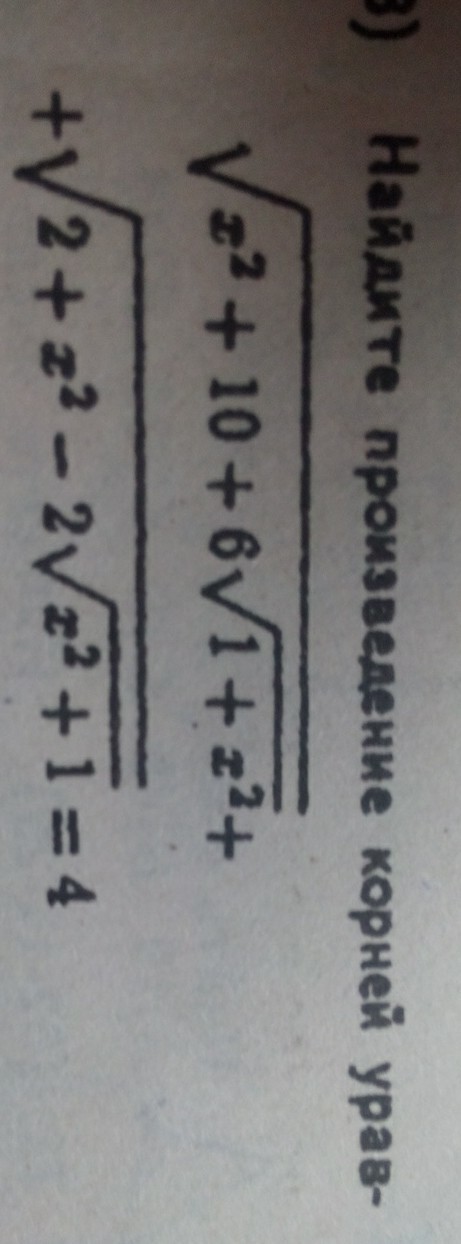
Ответы
Автор ответа:
0
Представим уравнение так:
 .
.
Используя формулы сокращенного умножения , получим
, получим


Модуля можно убрать, т.к. под модульные выражения будут принимать всегда положительные значения для всех х

Ответ: х = 0.
Используя формулы сокращенного умножения
Модуля можно убрать, т.к. под модульные выражения будут принимать всегда положительные значения для всех х
Ответ: х = 0.
Автор ответа:
0
Если быть точным, то подмодульные выражения всегда будут принимать неотрицательные значения, т.к. при х=0 второй модуль равен 0.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Литература,
автор: hazhetovkairzhan
Предмет: Математика,
автор: vanisimova253
Предмет: Математика,
автор: цук3