Question

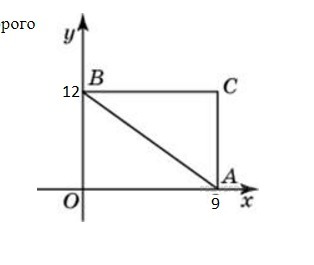
Найдите абсциссу центра окружности (см. рис.), описанной около треугольника, вершины которого имеют координаты (9;0),(0;12),(9;12).

Answer 1

Это задача из ЕГЭ. Рисунок, который не прикрепили, в приложении.
Допустим,что :точка А имеет координаты (9;0), В(0;12),С(9;12).
Найдём длину сторон треугольника АВ,АС,СВ:
$z= \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$
$AB= \sqrt{(0-9)^2+(12-0)^2}= \sqrt{9^2+12^2}= \sqrt{81+144}= \sqrt{225}=15$
$AC= \sqrt{(9-9)^2+(12-0)^2}= \sqrt{12^2}= 12$
$CB= \sqrt{(0-9)^2+(12-12)^2}= \sqrt{9^2}= 9$
Как мы видим, отношение сторон нашего треугольника равно 3;4;5 - отсюда следует, что этот треугольник прямоугольный(9/12=3/4,12/15=4/5). 
У прямоугольного треугольника центр окружности лежит на средине гипотенузы.
Гипотенуза это наибольшая сторона т.е АВ
$x_{m} = \frac{9+0}{2}=4,5$
$y_m= \frac{12+0}{2} =6$
абсцисса это точка Х