Предмет: Алгебра,
автор: Змей24
 Задание повышенной сложности, 11 класс. Решить в рамках школьной программы, правило Лопиталя использовать нельзя.
Задание повышенной сложности, 11 класс. Решить в рамках школьной программы, правило Лопиталя использовать нельзя.
Ответы
Автор ответа:
0
Подставив вместо х=п/2, получим  . Если неопределенность
. Если неопределенность  , то работаем всегда со вторым замечательным пределом
, то работаем всегда со вторым замечательным пределом 

Приложения:
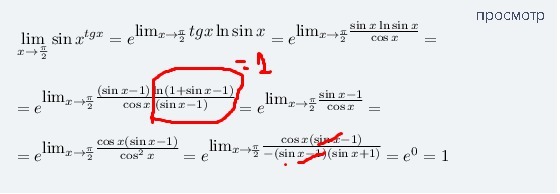
Похожие вопросы
Предмет: Алгебра,
автор: tea66
Предмет: Информатика,
автор: kristinaprygunova98
Предмет: Астрономия,
автор: kirill010000
Предмет: Литература,
автор: skachcovva
Предмет: Биология,
автор: яна1213141