Предмет: Геометрия,
автор: Dимасuk
Постройте равноугольно-полуправильный шестиугольник, у которого стороны относятся как 2:1. Опишите около него окружность и выразите её радиус через стороны шестиугольника.
(Построение, этапы построения и формулы)
Ответы
Автор ответа:
0
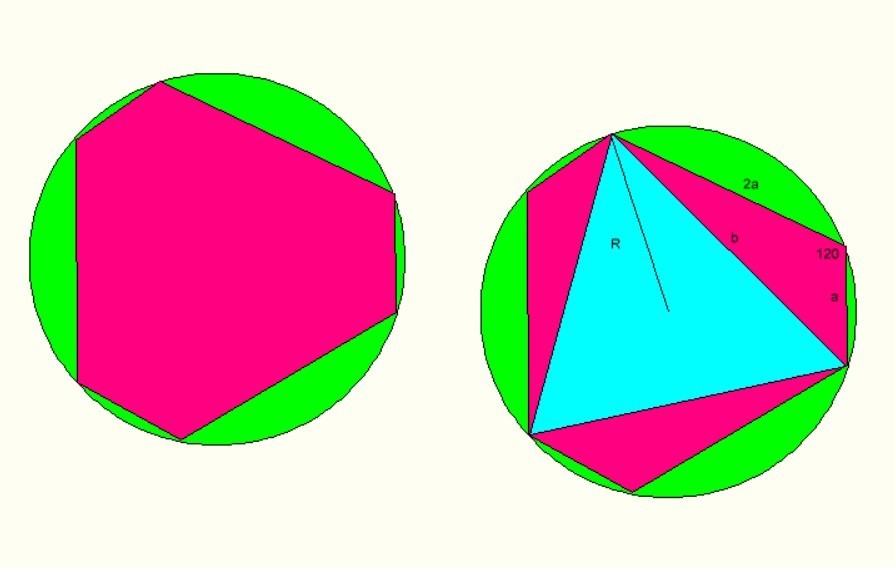
у шестиугольника стороны под углами 120, соединим по две вершины шестиугольника так чтобы получился равносторонний треугольник. его сторона по теореме косинусов
в=а*корень(5-2*соs(120)) =а*корень(5+2*соs(60)) =а*корень(6)
радиус описанной около равностороннего треугольника окружности известен R=b/корень(3)=а*корень(2) где а - меньшая сторона а 2а - болшая сторона шестиугольника
в=а*корень(5-2*соs(120)) =а*корень(5+2*соs(60)) =а*корень(6)
радиус описанной около равностороннего треугольника окружности известен R=b/корень(3)=а*корень(2) где а - меньшая сторона а 2а - болшая сторона шестиугольника
Приложения:
Автор ответа:
0
Спасибо большой!)
Автор ответа:
0
большое*
Автор ответа:
0
рисунок прилагается
Автор ответа:
0
расчеты перепроверьте - мог ошибиться
Автор ответа:
0
всё правильно :)
Похожие вопросы
Предмет: Геометрия,
автор: arinasahbazova32
Предмет: Алгебра,
автор: nastailla58
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Литература,
автор: vika508