Question

Площадь основания цилиндра относится к площади его осевого сечения как π:4 . Найдите периметр осевого сечения, если радиус основания цилиндра равен 6 см.

Answer 1

Задание. Площадь основания цилиндра относится к площади его осевого сечения как π:4 . Найдите периметр осевого сечения, если радиус основания цилиндра равен 6 см.
        Решение:
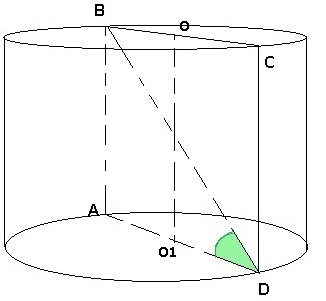
В основе лежит окружность, т.е. площадь основания равна $\pi R^2$. Осевым сечением является прямоугольник ABCD, AD - диаметр основания. Площадь осевого сечения равна $AB\cdot AD=h\cdot 2R$

Их отношения: $\dfrac{ \pi R^2}{2Rh} = \dfrac{\pi}{4} ;\,\,\,\,\,\,\,\, \dfrac{3}{h} = \dfrac{1}{4} ;$   откуда    $h=12$ см
AD = 2*R = 2 * 6 = 12 см.

Периметр осевого сечения равен $2(AD+AB)=2\cdot(12+12)=48\,\, _{CM}$

Ответ: 48 см.

Answer 2

Sоснования=36п, S осевого сечения =12Х
36п/12Х=п:4
Х=12
Р осевого сечения =(12+12)*2=48