Предмет: Геометрия, автор: Аноним

В трапеции ABCD точка M лежит на середине боковой стороны AB, диагональ BD пересекает отрезок CM в точке O. Найти площадь треугольника COD, если площадь треугольника BOM равна 1 и CO:OM=1:4.

Аноним: К вашему сожалению, я не склерозник и решение запомнил, а вот от вас хотел бы увидеть решение лучше, раз то было неверно

marshal500: У меня нет никакого сожаления по поводу удаления ответа на ваш вопрос. Треугольники, подобие которых пытались доказать (на тщетно), могут быть подобны только если стороны, против вертикальных углов, параллельны. Это может быть только при равнобедренной трапеции вида параллелограмма. Чертеж выполнен неправильно, отсюда и затруднение с выкладками.

Аноним: Почему это стороны против верт

Аноним: Верт. Углов должны быть параллельны

Аноним: Равноб. трапеция вида параллелограмма? Что? В трапеции по определению 1 пара сторон не может быть параллельна. Этим она от параллелограмма и отличается

marshal500: У подобных треугольников соответственные углы равны.

marshal500: Треугольники в вашем задании не могут бать подобны если их стороны не параллельны.

Аноним: В 99,9% случаев подобные треугольники не имеют параллельных частей

marshal500: Это в том случае если эти треугольники не имеют общих вертивальных углов.

Аноним: Без вертикальных как правило и требуется доказать

Ответы

Автор ответа: Denik777

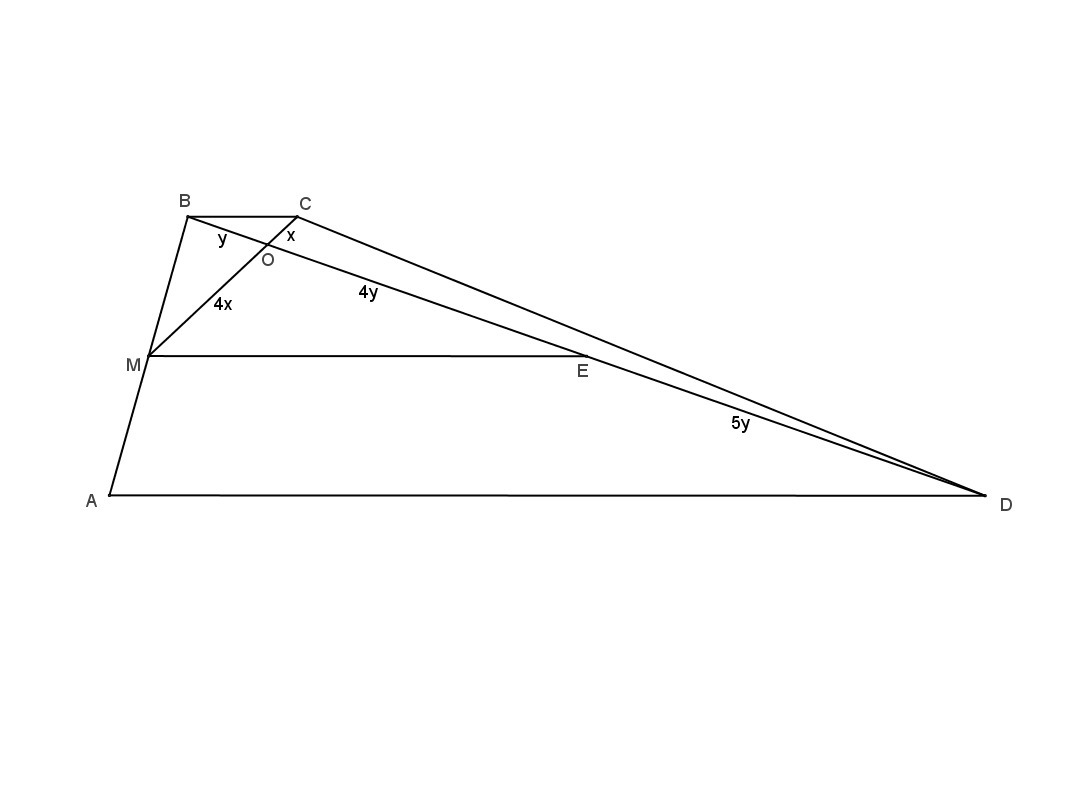
Пусть Е - середина BD, тогда треугольники BOC и EOM подобны (ME||AD как ср. линия треугольника ABD). Т.к. CO:OM=1:4, то BO=y, OE=4y и DE=BE=5y, т.е. OD=9y.
Т.к. треугольники BOC и BOM имеют общую высоту, а их основания относятся как 1:4, то S(BOC)=S(BOM)/4=1/4. Аналогично, для треугольников DOC и BOC, получаем S(DOC)=9S(BOC)=9/4.

Приложения: