Предмет: Математика,
автор: Алкадиеныч
Решить параметр. На фотографии. Подробно.
Приложения:
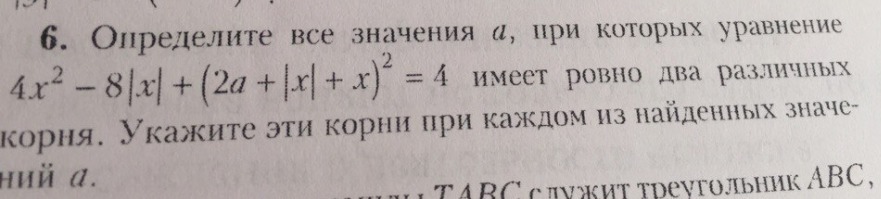
Ответы
Автор ответа:
4
4x^2 - 8|x| + (2a + |x| + x)^2 = 4
1) При x < 0 будет |x| = -x; |x| + x = 0
4x^2 + 8x + (2a)^2 = 4
4x^2 + 8x + 4a^2 - 4 = 0
x^2 + 2x + a^2 - 1 = 0
D/4 = 1 - a^2 + 1 = 2 - a^2
Если уравнение имеет 2 корня, то D/4 > 0
2 - a^2 > 0
a^2 < 2
a ∈ (-√2; √2)
Но реально будет 2 корня, только если они оба меньше 0, по условию.
x1 = -1 - √(2 - a^2) < 0 - это верно при любом а ∈ (-√2; √2)
x2 = -1 + √(2 - a^2) < 0
√(2 - a^2) < 1
2 - a^2 < 1
a^2 > 1
a ∈ (-√2; -1) U (1; √2)
2) При x >= 0 будет |x| = x; |x| + x = 2x
4x^2 - 8x + (2a + 2x)^2 = 4
4x^2 - 8x + 4(a + x)^2 - 4 = 0
x^2 - 2x - 1 + (x^2 + 2ax + a^2) = 0
2x^2 + 2(a - 1)x + (a^2 - 1) = 0
D/4 = (a - 1)^2 - 2(a^2 - 1) = a^2 - 2a + 1 - 2a^2 + 2 = -a^2 - 2a + 3
Если уравнение имеет 2 корня, то D/4 > 0
-a^2 - 2a + 3 = -(a - 1)(a + 3) > 0
a ∈ (-3; 1)
Но реально будет 2 корня, только если они оба больше 0, по условию.
x1 = (1 - a + √(-a^2-2a+3))/2 >= 0 - это верно при любом a ∈ (-3; 1)
x2 = (1 - a - √(-a^2-2a+3))/2 >= 0
1 - a - √(-a^2 - 2a + 3) >= 0
√(-a^2 - 2a + 3) <= 1 - a
-a^2 - 2a + 3 <= a^2 - 2a + 1
2a^2 >= 2; a^2 >= 1
a ∈ (-3; -1] U [1]; значения a > 1 не входят в промежуток a ∈ (-3; 1).
Таким образом, при a ∈ (-√2; -1) будет 4 корня - 2 меньше 0 и 2 больше 0.
Ответ: a ∈ (-3; -√2) U [1; √2)
1) При x < 0 будет |x| = -x; |x| + x = 0
4x^2 + 8x + (2a)^2 = 4
4x^2 + 8x + 4a^2 - 4 = 0
x^2 + 2x + a^2 - 1 = 0
D/4 = 1 - a^2 + 1 = 2 - a^2
Если уравнение имеет 2 корня, то D/4 > 0
2 - a^2 > 0
a^2 < 2
a ∈ (-√2; √2)
Но реально будет 2 корня, только если они оба меньше 0, по условию.
x1 = -1 - √(2 - a^2) < 0 - это верно при любом а ∈ (-√2; √2)
x2 = -1 + √(2 - a^2) < 0
√(2 - a^2) < 1
2 - a^2 < 1
a^2 > 1
a ∈ (-√2; -1) U (1; √2)
2) При x >= 0 будет |x| = x; |x| + x = 2x
4x^2 - 8x + (2a + 2x)^2 = 4
4x^2 - 8x + 4(a + x)^2 - 4 = 0
x^2 - 2x - 1 + (x^2 + 2ax + a^2) = 0
2x^2 + 2(a - 1)x + (a^2 - 1) = 0
D/4 = (a - 1)^2 - 2(a^2 - 1) = a^2 - 2a + 1 - 2a^2 + 2 = -a^2 - 2a + 3
Если уравнение имеет 2 корня, то D/4 > 0
-a^2 - 2a + 3 = -(a - 1)(a + 3) > 0
a ∈ (-3; 1)
Но реально будет 2 корня, только если они оба больше 0, по условию.
x1 = (1 - a + √(-a^2-2a+3))/2 >= 0 - это верно при любом a ∈ (-3; 1)
x2 = (1 - a - √(-a^2-2a+3))/2 >= 0
1 - a - √(-a^2 - 2a + 3) >= 0
√(-a^2 - 2a + 3) <= 1 - a
-a^2 - 2a + 3 <= a^2 - 2a + 1
2a^2 >= 2; a^2 >= 1
a ∈ (-3; -1] U [1]; значения a > 1 не входят в промежуток a ∈ (-3; 1).
Таким образом, при a ∈ (-√2; -1) будет 4 корня - 2 меньше 0 и 2 больше 0.
Ответ: a ∈ (-3; -√2) U [1; √2)
Похожие вопросы
Предмет: Информатика,
автор: kriskristina590
Предмет: Українська мова,
автор: karpenkomaksim695
Предмет: Физика,
автор: Pekaop
Предмет: Математика,
автор: abajdukova818