Предмет: Геометрия,
автор: polischuck
Допоможіть будь ласка!!!
З точки кола В проведено дві хорди ВА і ВС завдовжки 10 см і 12 см відповідно. Обчислити радіус кола, описаного навколо трикутника АВС, якщо відстань від середини меншої хорди до більшої хорди дорівнює 4 см.
Ответы
Автор ответа:
0
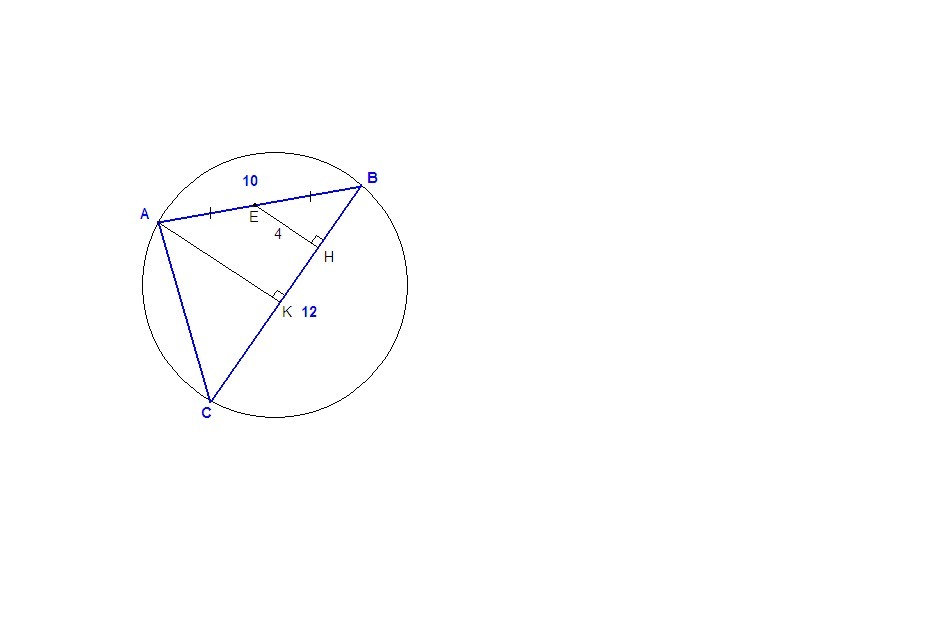
Пусть Е - середина АВ.
АЕ = ЕВ = 5 см
Проведем ЕН⊥ВС и АК⊥ВС. Тогда ЕН║АК.
ЕН = 4 см.
ΔЕНВ прямоугольный, Египетский, ⇒ НВ = 3 см.
ЕН - средняя линия ΔАКВ, тогда ВК = 2ВН = 6 см
Значит, АК - высота и медиана треугольника АВС, значит он равнобедренный,
АС = АВ = 10 см
Из ΔЕНВ sin∠EBH = 4/5
AC/sin∠ABC = 2R, где R - радиус описанной окружности.
10/(4/5) = 2R
R = 50/8 = 25/4 = 6,25 см
АЕ = ЕВ = 5 см
Проведем ЕН⊥ВС и АК⊥ВС. Тогда ЕН║АК.
ЕН = 4 см.
ΔЕНВ прямоугольный, Египетский, ⇒ НВ = 3 см.
ЕН - средняя линия ΔАКВ, тогда ВК = 2ВН = 6 см
Значит, АК - высота и медиана треугольника АВС, значит он равнобедренный,
АС = АВ = 10 см
Из ΔЕНВ sin∠EBH = 4/5
AC/sin∠ABC = 2R, где R - радиус описанной окружности.
10/(4/5) = 2R
R = 50/8 = 25/4 = 6,25 см
Приложения:
Похожие вопросы
Предмет: Химия,
автор: pubg95
Предмет: История,
автор: idiplus
Предмет: Українська література,
автор: milanaparasic
Предмет: Математика,
автор: ЭлькаКаромелька