Предмет: Алгебра,
автор: HoldUpPls
Решить уравнение для каждого параметра а:
a^2x+1=|x|+a
Даю 15 баллов))
Ответы
Автор ответа:
0
Рассмотрим функции  и
и 
Угловые коэффициенты функции g(x) = |x| равны 1 и -1, т.е. f(x) будет параллельным к графику g(x) если угловые коэффициенты совпадают:
1) , то
, то  и
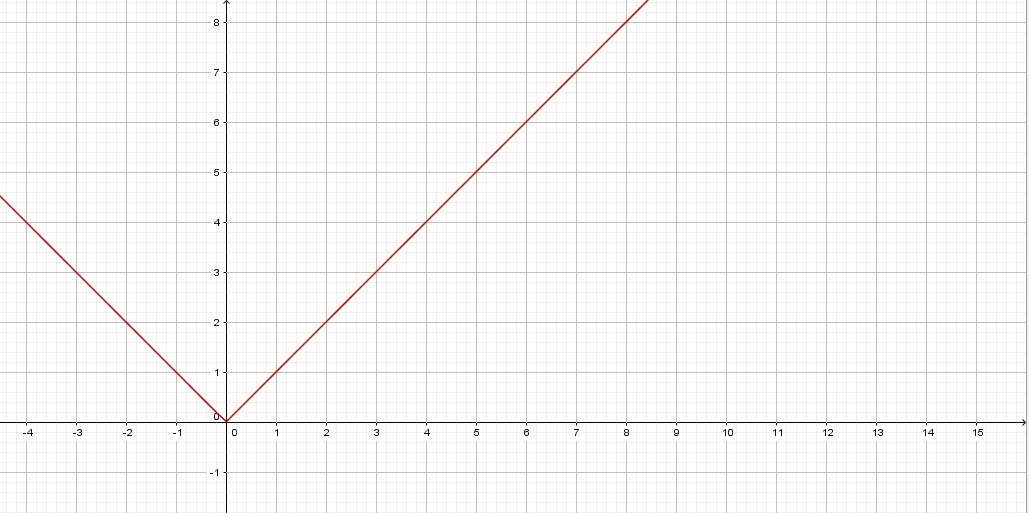
и  . График функции f(x) совпадает с графиком функции g(x) при x≥0
. График функции f(x) совпадает с графиком функции g(x) при x≥0
Решением уравнения есть все значения х из
2) Если а=-1, то - прямая, которая проходит через точки (0;2) и (-2;0). График функции f(x) = x+2 параллельный графику функции f(x)=|x| при x≥0, f(x) с g(x) пересекаются в одной точке
- прямая, которая проходит через точки (0;2) и (-2;0). График функции f(x) = x+2 параллельный графику функции f(x)=|x| при x≥0, f(x) с g(x) пересекаются в одной точке
Исходя из этого мы можем сделать вывод, что при![a in (-infty;-1]cup[1;+infty) a in (-infty;-1]cup[1;+infty)](https://tex.z-dn.net/?f=a+in+%28-infty%3B-1%5Dcup%5B1%3B%2Binfty%29) уравнение имеет одно решение.
уравнение имеет одно решение.
При уравнение имеет 2 решения.
уравнение имеет 2 решения.
Угловые коэффициенты функции g(x) = |x| равны 1 и -1, т.е. f(x) будет параллельным к графику g(x) если угловые коэффициенты совпадают:
1)
Решением уравнения есть все значения х из
2) Если а=-1, то
Исходя из этого мы можем сделать вывод, что при
При
Приложения:
Автор ответа:
0
Произведение множителей равно нулю, если любой из множителей равен нулю.
Если a = 0 или 1, то x ∈ [0; +∞).
Если a ≠ 0, a ≠ 1. то x = 0.
Итак, если a ≤ 1, то x = (a - 1)/(a² + 1).
Ответ: если a = 0, то x ∈ [0; +∞) или x = (a - 1)/(a² + 1); если a = 1, то x ∈ [0; +∞) или x = (a - 1)/(a² + 1); если a ∈ (-∞; 0) U (0; 1), то x = (a - 1)/(a² + 1), или x = 0.
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: vinihenkonik6
Предмет: Алгебра,
автор: korolevis108
Предмет: Русский язык,
автор: ivashka81
Предмет: Химия,
автор: мавус