Question

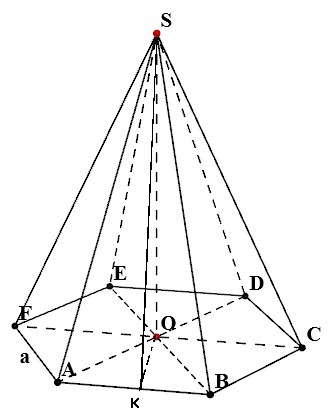
Прошу помочь решить задачу с пирамидой.

Answer 1

Объем пирамиды вычисляется по формуле $V= frac{1}{3} Socdot SO$, где So - площадь основания, SO - высота пирамиды.

Поскольку шестиугольная пирамида правильна, то в основе лежит правильный шестиугольник, то сторона основания равен $sqrt{ dfrac{2S_o sqrt{3} }{9} } = sqrt{ dfrac{2cdot frac{27 sqrt{3} }{2} cdot sqrt{3} }{9} } =3$. Тогда радиус вписанной окружности основания $r=frac{1}{2} a sqrt{3} =frac{1}{2}3 sqrt{3}$.

Из прямоугольного треугольника SOK по т. Пифагора найдем высоту пирамиды SO, т.е. $SO= sqrt{SK^2-OK^2} = sqrt{( frac{1}{2} sqrt{283})^2-( frac{1}{2} 3sqrt{3} )^2 } =8$

Найдем объем пирамиды) $V= dfrac{1}{3} cdot dfrac{27sqrt{3} }{2} cdot8=36 sqrt{3}.$

Ответ: $36 sqrt{3}$