Предмет: Математика,
автор: Trikha
Прошу помочь с решением системы.
Приложения:
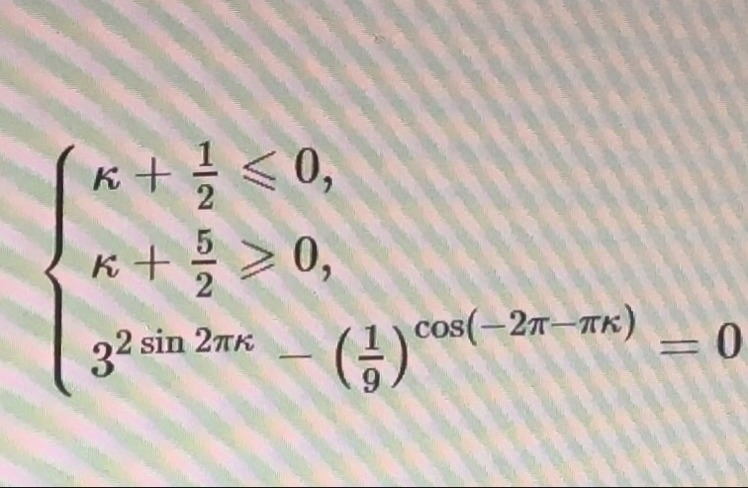
Ответы
Автор ответа:
0
в итоге получим:
при этом
значит можно с легкостью найти все значения значения k:
Ответ:
Похожие вопросы
Предмет: География,
автор: Ivannakovach
Предмет: Литература,
автор: egorefremov207
Предмет: Математика,
автор: Teddysh
Предмет: Химия,
автор: shutowski
Предмет: Алгебра,
автор: Аноним