Предмет: Алгебра,
автор: TheRazzy
Даю 30 балов. Номер 8,9,10,11
Приложения:
Ответы
Автор ответа:
0
8. Оскільки точка А належить графіку функції  , то прирівнявши ординати, маємо
, то прирівнявши ординати, маємо  . Помноживши обидві частини рівняння на 3*(3х+3), будемо мати наступне рівняння
. Помноживши обидві частини рівняння на 3*(3х+3), будемо мати наступне рівняння  . Спростивши рівняння до наступного вигляду
. Спростивши рівняння до наступного вигляду  дістанемо абсцису
дістанемо абсцису 
Отже, належить графіку заданої функції
належить графіку заданої функції
Відповідь:
9. Застосувавши означення модуля, маємо наступне рівняння .
.
Розглянемо такі випадки.
Випадок 1. маємо
маємо  . Знову за означенням абсолютної величини, маємо
. Знову за означенням абсолютної величини, маємо  звідки
звідки 
Випадок 2. тоді рівняння перепишемо у наступному вигляді
тоді рівняння перепишемо у наступному вигляді  . Оскільки ліва частина рівнянні приймає невід'ємні значення, а права - від'ємне число, то рівняння розв'язків не має.
. Оскільки ліва частина рівнянні приймає невід'ємні значення, а права - від'ємне число, то рівняння розв'язків не має.
Відповідь: 10; -6.
10. Число остання цифра степені чергуються так: 3, 9, 1, 7, 3, 9, ... Тобто, цифра степені залежить від того, з якою остачею показник степені ділиться на 4, значить
остання цифра степені чергуються так: 3, 9, 1, 7, 3, 9, ... Тобто, цифра степені залежить від того, з якою остачею показник степені ділиться на 4, значить  закінчується цифрою 3, а число
закінчується цифрою 3, а число  - цифрою 5. То різниця цих чисел закінчується цифрою 8
- цифрою 5. То різниця цих чисел закінчується цифрою 8
Відповідь: 8.
11. . Перенесемо все в ліву частину
. Перенесемо все в ліву частину  , застосувавши формулу скороченого множення
, застосувавши формулу скороченого множення  , маємо
, маємо  . Спростивши все, маємо
. Спростивши все, маємо 
Добуток дорівнює нулю, якщо один із множників дорівнює нулю
 , виразимо через у, маємо
, виразимо через у, маємо 
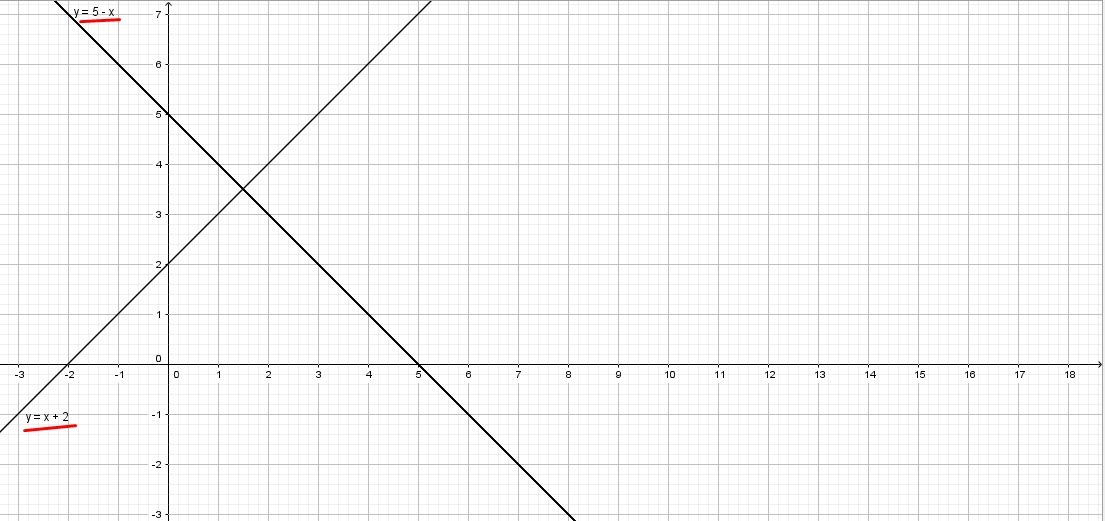
y=x+2 - пряма, яка проходить через точки (-2;0) і (0;2).
y=5-x - пряма, яка проходить через точки (5;0) і (0;5).
Отже,
Відповідь:
9. Застосувавши означення модуля, маємо наступне рівняння
Розглянемо такі випадки.
Випадок 1.
Випадок 2.
Відповідь: 10; -6.
10. Число
Відповідь: 8.
11.
Добуток дорівнює нулю, якщо один із множників дорівнює нулю
y=x+2 - пряма, яка проходить через точки (-2;0) і (0;2).
y=5-x - пряма, яка проходить через точки (5;0) і (0;5).
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: ar2r2j
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: karolina4542
Предмет: Математика,
автор: ddaaassswfreerthty
Предмет: Математика,
автор: zlata2128