Предмет: Алгебра,
автор: smirnovar2016
решите уравнение по алгебре
Приложения:
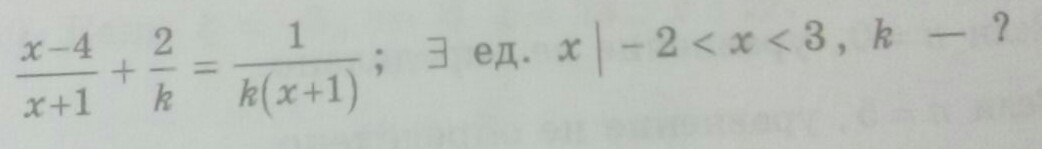
Ответы
Автор ответа:
1
отдельно решаем последнюю систему, используя подсказки, данные в задании:
во-первых,
во-вторых, попытаемся оценить, между какими числами находится дробь
последнее решим по отдельности, записав систему
итак, ответ:
1. корень уравнения
2. параметр
Автор ответа:
0
ОДЗ
{k≠0
{x+1≠0⇒x≠-1
k(x-4)+2(x+1)=1
kx-4k+2x+2=1
x(k+2)=4k-1
x=(4k-1)/(k+2)
{(4k-1)/(k+2)>-2
{(4k-1)/(k+2)<3
{k≠0
{(4k-1)/(k+2)≠-1
1)(4k-1)/(k+2)+2>0
(4k-1+2k+4)/(k+2)>0
(6k+3)/(k+2)>0
k=-0,5 k=-2
k<-2 U k>-0,5
2)(4k-1)/(k+2)-3<0
(4k-1-3k-6)/(k+2)<0
(k-7)/(k+2)<0
k=7 k=-2
-2<k<7
3)k≠0
4)(4k-1)/(k+2)≠-1
4k-1≠-k-2
4k+k≠-2+1
5k≠-1
k≠-0,2
\\\\\\\\\\\\\\\\\ //////////////////////////////////////////////////////////
----------(-2)---------(-0,5)-------(-0,2)----------(0)---------(7)--------
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
k∈(-0,5;-0,2) U (-0,2;0) U (0;7)
{k≠0
{x+1≠0⇒x≠-1
k(x-4)+2(x+1)=1
kx-4k+2x+2=1
x(k+2)=4k-1
x=(4k-1)/(k+2)
{(4k-1)/(k+2)>-2
{(4k-1)/(k+2)<3
{k≠0
{(4k-1)/(k+2)≠-1
1)(4k-1)/(k+2)+2>0
(4k-1+2k+4)/(k+2)>0
(6k+3)/(k+2)>0
k=-0,5 k=-2
k<-2 U k>-0,5
2)(4k-1)/(k+2)-3<0
(4k-1-3k-6)/(k+2)<0
(k-7)/(k+2)<0
k=7 k=-2
-2<k<7
3)k≠0
4)(4k-1)/(k+2)≠-1
4k-1≠-k-2
4k+k≠-2+1
5k≠-1
k≠-0,2
\\\\\\\\\\\\\\\\\ //////////////////////////////////////////////////////////
----------(-2)---------(-0,5)-------(-0,2)----------(0)---------(7)--------
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
k∈(-0,5;-0,2) U (-0,2;0) U (0;7)
Похожие вопросы
Предмет: Українська література,
автор: iakovenko146
Предмет: Математика,
автор: ermakliza26
Предмет: Математика,
автор: ssamoylov761
Предмет: Українська мова,
автор: kimimiki050809