Предмет: Геометрия,
автор: Знания
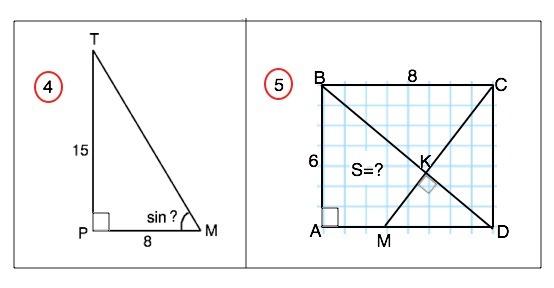
4. Найдите синус угла М треугольник МРТ, если угол Р - прямой, МР=8см, РТ=15см.
5. Стороны АВ и ВС прямоугольника АВСD равны 6см и 8 см. Прямая, проходящая через вершину С и перпендикулярная к прямой BD, пересекает сторону AD в точке М, а диагональ BDв точке К. Найдите площадь четырёхугольника АВМК.
Ответы
Автор ответа:
2
К задачам приложены рисунки.
4) sin∠ PMT=PT:MT
MT=17 ( прямоугольный треугольник из Пифагоровых троек)
sin∠PMT=15/17
5) Площадь четырехугольника АВКМ равна ∆ АВD минус площадь прямоугольного треугольника МКD.
Площадь АВD=S ABCD:2=6•8:2=24 см²
КС ⊥ВD, ⇒ КD в ∆ МСD перпендикулярна СМ и делит ∆ МСD на два подобных треугольника, ⇒ ∠КСD=∠КDМ.
BD =10 см ( ∆ АВD- египетский, можно и по т.Пифагора найти).
sin∠KCD=sin∠ADB=АВ:BD=0,6
КD=CD•sinKCD=6•0,6=3,6
tg∠KDM=tg∠BDM=6/8=3/4
MK=KD•tgKDM=3,6•3/4=2,7
S∆ KDM=KM•KD:2=3,6•2,7:2=4,86 см ² ⇒
S (АВКМ)= 24-4,86=19,14 см²
Приложения:
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Физика,
автор: Andriy17337
Предмет: Математика,
автор: sabinamuradilova22
Предмет: Химия,
автор: Hsquad06
Предмет: Алгебра,
автор: gocs7373333