Предмет: Алгебра,
автор: Ilyasssssss
нужно полное решение.
Приложения:
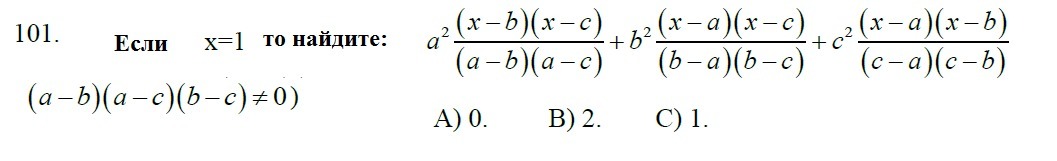
Ilyasssssss:
а почему из списка убрали?
Это выражение - квадратный трехчлен f(x). Очевидно f(a)=a^2, f(b)=b^2, f(c)=c^2. Поэтому, f(x)=x^2, т.е. f(1)=1.
можно подробней?
В принципе все уже написано. Подставьте а, b, c вместо х, Получится a^2, b^2, c^2. Кроме того х входит в выражение только во второй степени, значит это квадратный трехчлен. По трем точкам он однозначно определяется, и очевидно, что x^2 удовлетворяет.
Ответы
Автор ответа:
2
Представим данное равенство в виде

приводим к общему знаменателю и выносим общий множитель

Получаем что 0 = 0. Квадратное уравнение при имеет бесконечно много решений, то есть, выполняется тождество. Можно заметить, что исходное уравнение, имеющее относительно х степень не выше, чем вторую, имеет более двух корней как
имеет бесконечно много решений, то есть, выполняется тождество. Можно заметить, что исходное уравнение, имеющее относительно х степень не выше, чем вторую, имеет более двух корней как 
приводим к общему знаменателю и выносим общий множитель
Получаем что 0 = 0. Квадратное уравнение при
значит ответ 1?
Похожие вопросы
Предмет: Математика,
автор: kosenkoveronika89
Предмет: География,
автор: sonyagenerelova
Предмет: Русский язык,
автор: zarinareks
Предмет: Информатика,
автор: marina13131986