Question

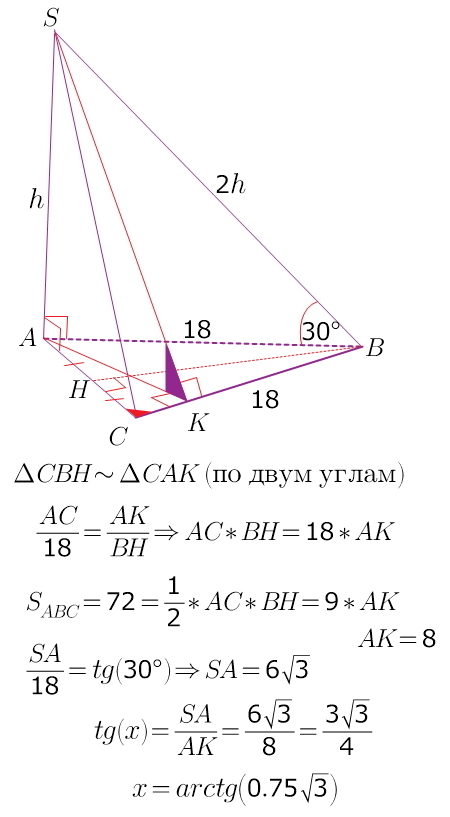
Прошу помочь с задачей .Основой пирамиды SABC является равнобедренный остроугольный треугольник ABC. AB=BC=18. Грани SAC и SAB перпендикулярны к площади основания пирамиды, а ребро SB наклонено к ней под углом 30 градусов. Определить угол между площадями (SBC) и (ABC), если площадь основания пирамиды равняется 72. Заранее спасибо

Answer 1

т.к. обе грани перпендикулярны основанию, 
их линия пересечения SА ⊥ (ABC), 
искомый угол --это линейный угол двугранного угла SBCA,  
он будет равен углу между перпендикулярами к ВС, лежащими в этих плоскостях...
две разные высоты любого равнобедренного треугольника образуют подобные прямоугольные треугольники))