Предмет: Математика,
автор: ssokolova
Помогите, пожалуйста.. Нужно решить одно уравнение и два неравенства
Приложения:
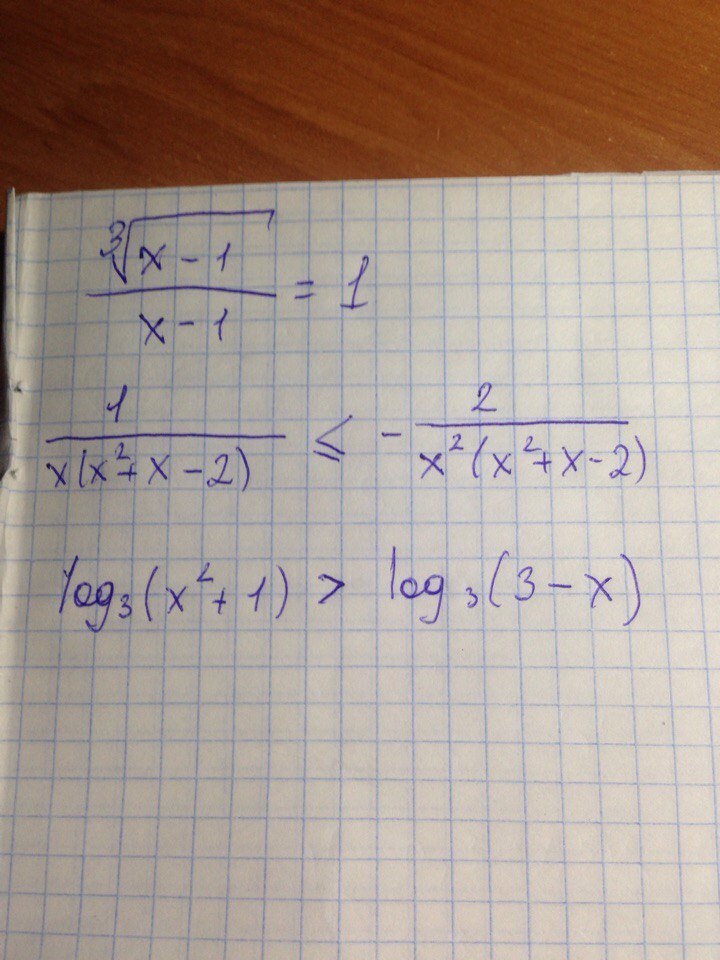
Ответы
Автор ответа:
1
1
∛(x-1)/∛(x-1)³=1
1/∛(x-1)²=1
x-1=1
x=2
2
1/x(x²=x-2)+2/x²(x²+x-2)≤0
(x+2)/x²(x²+x-2)≤0
x²+x-2=0
x1+x2=-1 U x1*x2=-2
x1=-2 U x2=1
(x+2)/[x²(x+2)(x-1)]≤0
1/x²(x-1)≤0,x≠-2
1>0⇒x²(x-1)<0
x=0 x=1
_ _ +
------------(-2)-----------------(0)------------(1)-------------------
x∈(-∞;-2) U (-2;0) U (0;1)
3
ОДЗ
{x²+1>0 при любом х
{3-x>0⇒x<3
x∈(-∞;3)
основания равны,значит
x²+1>3-x
x²+x-2>0
x1+x2=-1 U x1*x2=-2
x1=-2 U x2=1
x<-2 U x>1
\\\\\\\\\\\\\\\\\\\\\\\\ //////////////////////////////////////
------------------(-2)---------------(1)---------------(3)---------
////////////////////////////////////////////////////////////////////////
x∈(-∞;-2) U (1;3)
∛(x-1)/∛(x-1)³=1
1/∛(x-1)²=1
x-1=1
x=2
2
1/x(x²=x-2)+2/x²(x²+x-2)≤0
(x+2)/x²(x²+x-2)≤0
x²+x-2=0
x1+x2=-1 U x1*x2=-2
x1=-2 U x2=1
(x+2)/[x²(x+2)(x-1)]≤0
1/x²(x-1)≤0,x≠-2
1>0⇒x²(x-1)<0
x=0 x=1
_ _ +
------------(-2)-----------------(0)------------(1)-------------------
x∈(-∞;-2) U (-2;0) U (0;1)
3
ОДЗ
{x²+1>0 при любом х
{3-x>0⇒x<3
x∈(-∞;3)
основания равны,значит
x²+1>3-x
x²+x-2>0
x1+x2=-1 U x1*x2=-2
x1=-2 U x2=1
x<-2 U x>1
\\\\\\\\\\\\\\\\\\\\\\\\ //////////////////////////////////////
------------------(-2)---------------(1)---------------(3)---------
////////////////////////////////////////////////////////////////////////
x∈(-∞;-2) U (1;3)
yugolovin:
В 1-м пункте потеряли x=0
В 3-м пункте важно не только то, что основания равны, но и то, что они больше 1. Иначе пришлось бы знак неравенства менять
Послать на исправление?
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: История,
автор: vitalinaystimenko1
Предмет: Алгебра,
автор: devo4kalapo4ka
Предмет: Українська мова,
автор: tenyaboronko