Question

Найдите наименьшее положительное значение параметра а, при котором система уравнений
y-|x+2|-|x-2|=0
y-ax+a-3=0
Имеет единственное решение

Answer 1

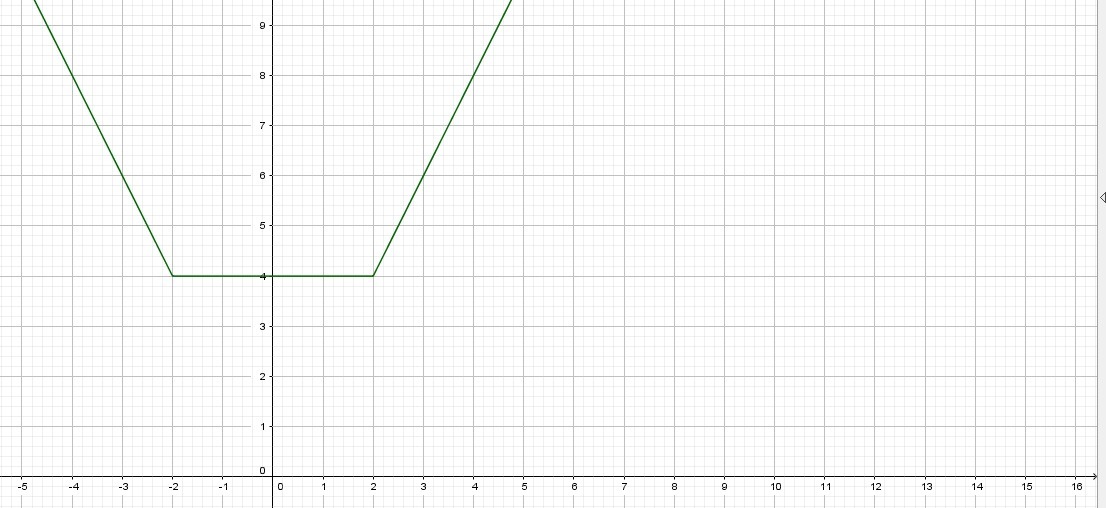
Построим график функции$y=|x+2|+|x-2|$

Для начала упростим функцию

Найдем знаки под модульного выражения

$\left[\begin{array}{ccc}x+2=0\\ x-2=0\end{array}\right\Rightarrow \left[\begin{array}{ccc}x_1=-2\\ x_2=2\end{array}\right$

_-__-__(-2)__+__-__(2)__+__+__

$y=|x+2|+|x-2|= \left[\begin{array}{ccc} \left \{ {{x \leq -2} \atop {-x-2-x+2}} \right. \\ \left \{ {{-2\ \textless \ x \leq 2} \atop {x+2-x+2}} \right. \\ \left \{ {{x\ \textgreater \ 2} \atop {x+2+x-2}} \right. \end{array}\right= \left[\begin{array}{ccc} \left \{ {{x \leq -2} \atop {-2x}} \right. \\ \left \{ {{-2\ \textless \ x \leq 2} \atop {4}} \right. \\ \left \{ {{x\ \textgreater \ 2} \atop {2x}} \right. \end{array}\right$

Наименьшее положительное значение параметра а найдем с помощью параллельности прямых

График функции $y=|x+2|+|x-2|$ параллельный прямой $y-ax+a-3=0$ если угловые коэффициенты будут совпадать, т.е. $k=\pm2$

Но нам важен положительный параметр, значит $a=2$ - минимальный.

Исследуем когда график будет касаться в точке (2;4) и (-2;4)

Подставив значения х=2 и у=4, получим

$4-2a+a-3=0\\ 1-a=0\\ a=1$

При а=1 система уравнений имеет одно решение

Если подставить $x=-2$ и $y=4$, получим

$4+2a+a-3=0\\ 3a=-1\\ a=- \frac{1}{3}$


Наименьший параметр а=1.