Question

Двугранные углы при основании правильной четырехугольной пирамиды равны 60 градусов. Найдите площадь боковой поверхности пирамиды, если сторона основания равна корень из2

Answer 1

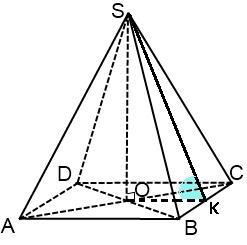
SABCD-правильная пирамида,SO-высота,SH_|_DC,<SHO=60,DC=√2
ΔSOH прямоугольный
OH=1/2*AB=√2/2
<OSH=90-<SHO=90-60=30⇒
OH=1/2*SH
SH=2*√2/2=√2
Sбок=4S(DSC)=4*1/2*DC*SH=2*√2*√2=4

b1594adf59e5ad18df9c25b1a8cf6fac.docx

Answer 2

∠SKO = 60°. AB=√2.

OK - радиус вписанной окружности основания ABCD

OK = AD/2 = √2/2.

Из прямоугольного треугольника SOK. Косинус - отношение прилежащего катета к гипотенузе

$\cos \angle OKS= \frac{OK}{SK}$   откуда   $SK= \frac{OK}{\cos 60а} =2\cdot \frac{ \sqrt{2} }{2} =\sqrt{2}$

Площадь одной грани найдем из треугольника SCB

$S_1= \frac{BC\cdot SK}{2} = \frac{\sqrt{2} \cdot\sqrt{2} }{2} =1$

У пирамиды 4 граней, значит площадь боковой равен 4*S₁ = 4 * 1 = 4

Ответ: 4.