Предмет: Алгебра,
автор: 0helpmeplease
Помогите упростить выражение.Срочно нужно:)
Приложения:
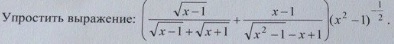
Ответы
Автор ответа:
1
1) Упростим вторую дробь


2)Упростим сумму дробей в скобках



3)И, наконец, умножение

Ответ: х²-1
2)Упростим сумму дробей в скобках
3)И, наконец, умножение
Ответ: х²-1
Похожие вопросы
Предмет: История,
автор: sslobodyan
Предмет: Литература,
автор: KlyBniLa13
Предмет: Английский язык,
автор: kika113
Предмет: История,
автор: Gulnas011107
Предмет: Алгебра,
автор: MammaevRabazan