Question

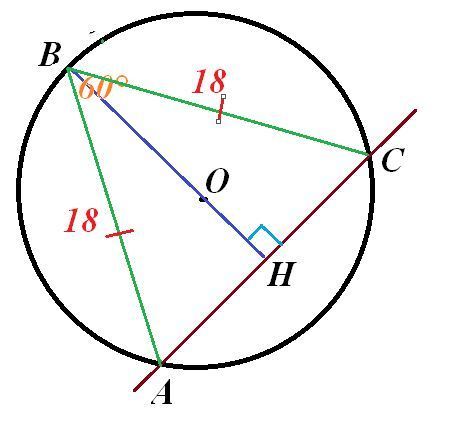
Вписанный угол ABC опирается на дугу, составляющую $\frac{1}{3}$ окружности; АВ = ВС = 18. Найдите расстояние от точки В до прямой АС.

Answer 1

1/3 окружности есть 360°:3=120°. Значит, дуга АС = 120°. Тогда величина вписанного угла АВС равна 120°:2=60°.
Рассмотрим ΔАВС. По условию ВА=ВС=18, значит, ΔАВС-равнобедренный с основанием АС. Следовательно, в ΔАВС ∠А=∠С=(180°-60°):2=60°.
То есть ΔАВС - равносторонний, АС=18.
Расстояние от В то АС - это длина высоты ВН в ΔАВС, которая является медианой. Тогда АН=СН=9.
По теореме Пифагора в ΔНВС ВН² = ВС² - СН².
$BH= \sqrt{18^2-9^2}= \sqrt{27*9} = 9\sqrt{3}$
Ответ: $9\sqrt{3}$