Предмет: Математика,
автор: nclsgnv
хэлп, товарищи
------------------------
Приложения:
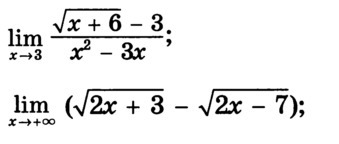
Ответы
Автор ответа:
1
1) Имеем неопределённость 0/0
Числитель и знаменатель умножаем на выражение сопряжённое числителю √(x+6) + 3, а в знаменателе выносим икс за скобку:
(√(x+6) - 3) (√(x+6) + 3) x - 3 1
-------------------------------- = ---------------------------- = ----------------------
x (x - 3) (√(x+6) + 3) x (x - 3) (√(x+6) + 3) x (√(x+6) + 3)
Теперь можно спокойно подставлять x->3 в полученное выражение, не боясь, что придётся ноль делть на ноль.
1 1
-------------------- = -----
3 (√(3+6) + 3) 18
2. При прямой подстановке x->+∞ имеем неопределённость (∞ - ∞). Из бесконечности вычитается бесконечность. Не всегда это будет равно нулю, т.к. выражения к бесконечности могут стремиться по разному.
Для решения воспользуемся тем же приёмом, что и в первом пределе, а именно умножим и разделим на сопряжённое выражение:
(√(2x+3) - √(2x-7)) * (√2x+3) + √(2x-7) 2x + 3 - (2x -7)
---------------------------------------------------- = -------------------------- =
√(2x+3) + √(2x-7) √(2x+3) + √(2x-7)
10
-------------------------
√(2x+3) + √(2x-7)
Теперь можно спокойно подставлять вместо икса бесконечность. В знаменателе будет ∞ + ∞ = ∞, т.е. при суммировании бесконечностей нет проблем, так и так получится бесконечность. В числителе у нас константа, если её разделить на бесконечность, получится ноль.
Итак, второй предел стремится к нулю.
Числитель и знаменатель умножаем на выражение сопряжённое числителю √(x+6) + 3, а в знаменателе выносим икс за скобку:
(√(x+6) - 3) (√(x+6) + 3) x - 3 1
-------------------------------- = ---------------------------- = ----------------------
x (x - 3) (√(x+6) + 3) x (x - 3) (√(x+6) + 3) x (√(x+6) + 3)
Теперь можно спокойно подставлять x->3 в полученное выражение, не боясь, что придётся ноль делть на ноль.
1 1
-------------------- = -----
3 (√(3+6) + 3) 18
2. При прямой подстановке x->+∞ имеем неопределённость (∞ - ∞). Из бесконечности вычитается бесконечность. Не всегда это будет равно нулю, т.к. выражения к бесконечности могут стремиться по разному.
Для решения воспользуемся тем же приёмом, что и в первом пределе, а именно умножим и разделим на сопряжённое выражение:
(√(2x+3) - √(2x-7)) * (√2x+3) + √(2x-7) 2x + 3 - (2x -7)
---------------------------------------------------- = -------------------------- =
√(2x+3) + √(2x-7) √(2x+3) + √(2x-7)
10
-------------------------
√(2x+3) + √(2x-7)
Теперь можно спокойно подставлять вместо икса бесконечность. В знаменателе будет ∞ + ∞ = ∞, т.е. при суммировании бесконечностей нет проблем, так и так получится бесконечность. В числителе у нас константа, если её разделить на бесконечность, получится ноль.
Итак, второй предел стремится к нулю.
nclsgnv:
огромное Вам спасибо
Похожие вопросы
Предмет: Математика,
автор: s68823738
Предмет: Английский язык,
автор: 1Елеонора2
Предмет: Химия,
автор: jrrux
Предмет: Қазақ тiлi,
автор: sagandykmalika
Предмет: Қазақ тiлi,
автор: narkyzberdesh