Предмет: Геометрия,
автор: diankaalashbai5031
СРОЧНО!
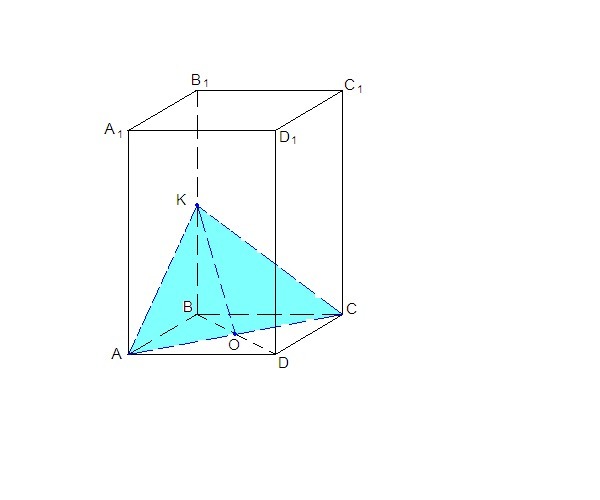
В правильной четырехугольной призме через диагональ основания и середину противолежащего бокового ребра проведено сечение. Найдите площадь сечения, если сторона основания 2 см, а ее высота 8 см
Ответы
Автор ответа:
1
В основании правильной четырехугольной призмы лежит квадрат. Диагональ квадрата
AC = BD = a√2 = 2√2 см ⇒ ОВ = √2 см (а - сторона квадрата)
К - середина ВВ₁, ⇒ ВК = ВВ₁/2 = 4 см
ΔКОВ: ∠В = 90°, по теореме Пифагора
ОК = √(ОВ² + ВК²) = √18 = 3√2 см
ВО⊥АС по свойству диагоналей квадрата, ВО - проекция КО на плоскость основания, ⇒ КО⊥АС, т.е. КО - высота сечения.
Sakc = AC·KO/2 = 2√2·3√2/2 = 6 см²
AC = BD = a√2 = 2√2 см ⇒ ОВ = √2 см (а - сторона квадрата)
К - середина ВВ₁, ⇒ ВК = ВВ₁/2 = 4 см
ΔКОВ: ∠В = 90°, по теореме Пифагора
ОК = √(ОВ² + ВК²) = √18 = 3√2 см
ВО⊥АС по свойству диагоналей квадрата, ВО - проекция КО на плоскость основания, ⇒ КО⊥АС, т.е. КО - высота сечения.
Sakc = AC·KO/2 = 2√2·3√2/2 = 6 см²
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: katerinamoroz701
Предмет: Математика,
автор: amiina0708
Предмет: Українська мова,
автор: t3rtyq
Предмет: Алгебра,
автор: ufyctcft4