Предмет: Алгебра,
автор: nclsgnv
необходимо решить уравнение:
Приложения:
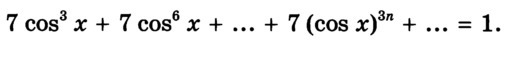
Ответы
Автор ответа:
1
здесь у нас сумма бесконечной геометрической прогрессии:










![cosx = \sqrt[3]{ \frac{1}{8} } cosx = \sqrt[3]{ \frac{1}{8} }](https://tex.z-dn.net/?f=cosx+%3D++%5Csqrt%5B3%5D%7B+%5Cfrac%7B1%7D%7B8%7D+%7D+)


Похожие вопросы
Предмет: Физика,
автор: qwertyys
Предмет: Геометрия,
автор: Аноним
Предмет: История,
автор: dpalik500
Предмет: Литература,
автор: OgaroV
Предмет: Английский язык,
автор: annaandreeva914