Предмет: Алгебра,
автор: lenarostovnd
Решить sin(a+b), если sin a = 8/17 и cos b = 4/5
Ответы
Автор ответа:
0
cosa=√(1-sin²a)=√(1-64/289)=√(225/289)=15/17
sinb=√(1-cos²b)=√(1-16/25)=√(9/25)=3/5
sin(a+b)=sina*cosb+cosa*sinb=8/17*4/5+15/17*3/5=32/85+45/85=77/85
sinb=√(1-cos²b)=√(1-16/25)=√(9/25)=3/5
sin(a+b)=sina*cosb+cosa*sinb=8/17*4/5+15/17*3/5=32/85+45/85=77/85
Автор ответа:
1
Раскрываем формулу
Потом просчитываем через теорему Пифагора
И в конце вставляем данные в развёрнутую формулу
Потом просчитываем через теорему Пифагора
И в конце вставляем данные в развёрнутую формулу
Приложения:
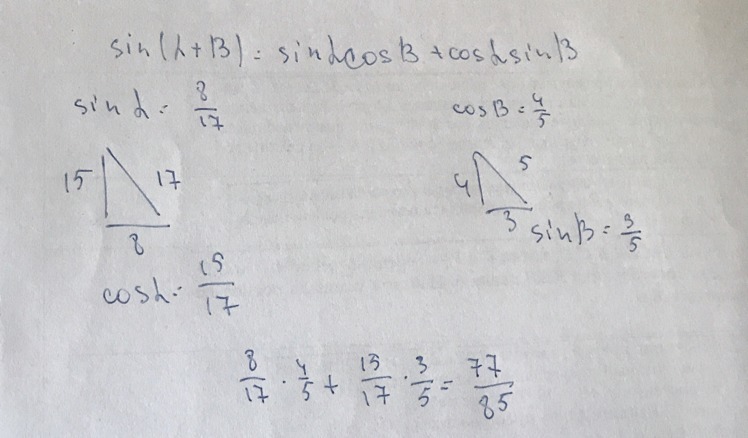
lenarostovnd:
Да, Пифагоровы тройки, точно!
Похожие вопросы
Предмет: Геометрия,
автор: lilianalexandrova197
Предмет: Алгебра,
автор: dashadeket9
Предмет: Английский язык,
автор: klumbkids
Предмет: Українська мова,
автор: vselifonova191