Предмет: Математика,
автор: valensokol8698
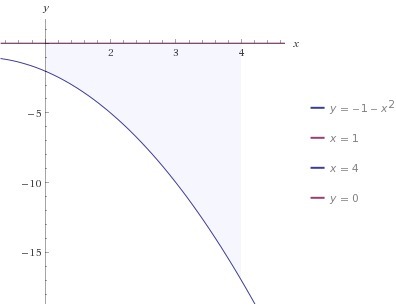
Вычислить площадь плоской фигуры ограниченной линиями:
у=-х^2-1, х=1, х=4, у=0
Ответы
Автор ответа:
1
пределы интегрирования уже заданны: x=1; x=4
находим площадь с помощью определенного интеграла:

Ответ: 24 ед²
находим площадь с помощью определенного интеграла:
Ответ: 24 ед²
Приложения:
Похожие вопросы
Предмет: Физика,
автор: angelinabagrij4
Предмет: Математика,
автор: Heatjshwaweknd
Предмет: Английский язык,
автор: ssasha77747
Предмет: Экономика,
автор: Stefarh