Предмет: Математика,
автор: veskass7ot753r
ПОМОГИТЕ решить, ПОЖАЛУЙСТА!!!!
Нужно найти производную
Приложения:
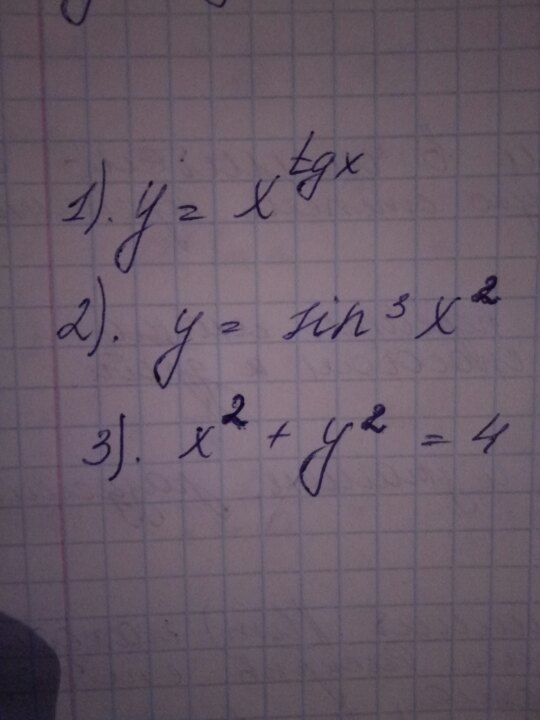
Ответы
Автор ответа:
0
1) y`=(x^tgx)
x^tgx=e^ln(x^tgx)=e^ln(x)tgx
u=ln(x)tgx (e^u)`=e^u
(e^ln(x)tgx)`=de^u/du*du/dx=(x^tgx)d(ln(x)tgx))/dx=lnx(dtgx/dx+dtgx/dx)x^tgx=(x^tgx)ln(x)/(cosx)^2+(tgx)/x)
2)y`=6xcos(x^2)(sin(x^2))^2
3) x^2+y^2=4
y^2=4-x^2
y=+-√(4-x^2)
y`=-x/√(4-x^2)
y`=x/√(4-x^2)
x^tgx=e^ln(x^tgx)=e^ln(x)tgx
u=ln(x)tgx (e^u)`=e^u
(e^ln(x)tgx)`=de^u/du*du/dx=(x^tgx)d(ln(x)tgx))/dx=lnx(dtgx/dx+dtgx/dx)x^tgx=(x^tgx)ln(x)/(cosx)^2+(tgx)/x)
2)y`=6xcos(x^2)(sin(x^2))^2
3) x^2+y^2=4
y^2=4-x^2
y=+-√(4-x^2)
y`=-x/√(4-x^2)
y`=x/√(4-x^2)
veskass7ot753r:
спасибо. А что такое (u) в первом примере?
новая переменная
Похожие вопросы
Предмет: Математика,
автор: slobodanukaleksandr7
Предмет: Биология,
автор: Аноним
Предмет: Українська література,
автор: vlados16062010
Предмет: Химия,
автор: Аноним