Question

Перша сторона трикутника дорівнює 30 см, а друга ділиться точкою дотику вписаного кола на відрізки 14 і 20 см, рахуючи від кінця першої сторони. Знайти площу трикутника.

Answer 1

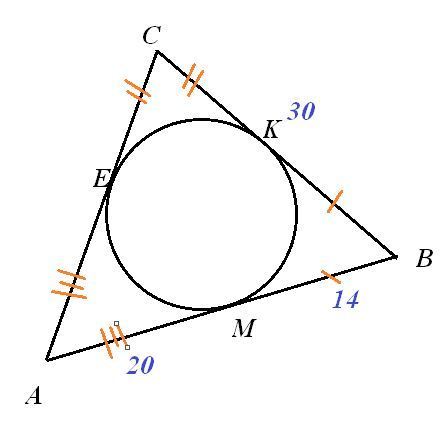
Пусть в ΔАВС вписана окружность. Е, К. М - точки касания окружности и сторон треугольника.
По свойству отрезков касательных к окружности, проведенных из одной точки: АЕ=АМ=20см, ВМ=ВК=14см, тогда СК=СЕ=30-14=16см.
Значит, стороны треугольника АВ=20+14=34см, ВС=30см, АС=20+16=36см.
Площадь ΔАВС по формуле Герона:
$p=\frac{a+b+c}{2},\ S_{\Delta} = \sqrt{p(p-a)(p-b)(p-c)}$
$p=\frac{34+36+30}{2}=50,\\ S_{\Delta} = \sqrt{50(50-34)(50-36)(50-30)} = \sqrt{50*16*14*20} =80 \sqrt{35}$
Ответ: $80 \sqrt{35}$ см²