Предмет: Геометрия,
автор: Afaxriya2001
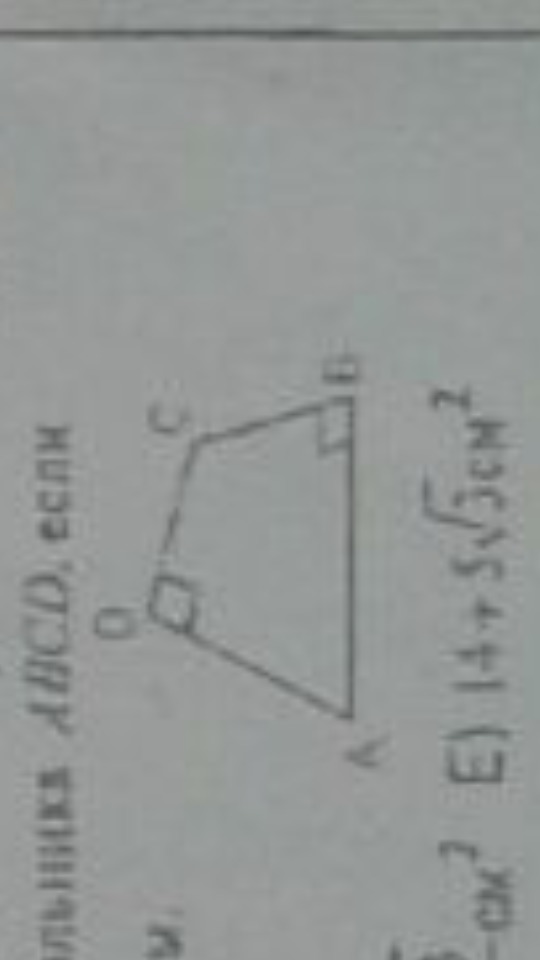
Найдите площадь четырехугольника ABCD, если AD =5корень из 3 АВ =8 и ВС=6
Ниже рисунок
Приложения:
Afaxriya2001:
Да, если можно
Дааа, Всё понятно!
Спасибо!!
Ответы
Автор ответа:
4
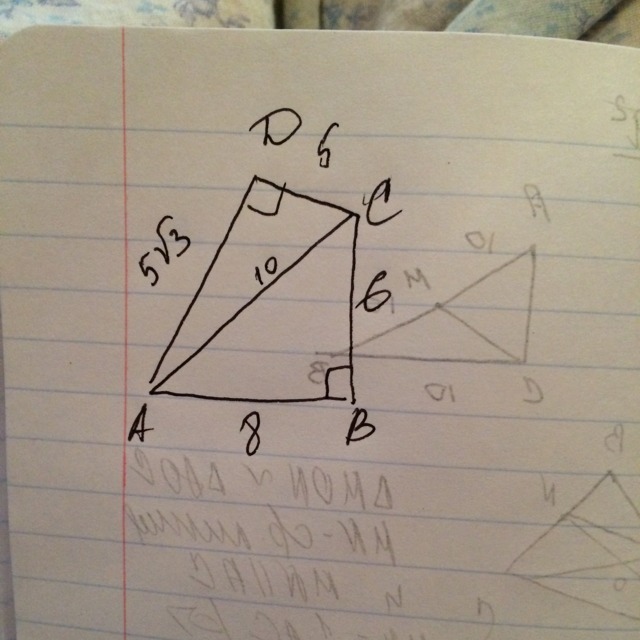
Проведём диагональ АС.
Этот отрезок делит четырёхугольник на 2 прямоугольных треугольника АДС и АВС.
Рассмотрим треугольник АВС.
Два катета по 6 и 8 соответсвенно.
По теореме Пифагора получаем, что гипотенуза АС= √100=10.
Площадь треугольника АВС= катет*катет/2=6*8/2=24.
Рассмотрим треугольник АДС.
Гипотенуза известна и равна 10. Катет равен 5√3.
По теореме Пифагора ищем второй катет.
Он равен= √(100-25*3)= √25=5.
Площадь треугольника АДС= 5*5√3/2=25√3/2
Площадь АВСД=площадь АВС+площадь АДС.
Площадь АВСД=(25√3)/2+24 Так. Объяснение, почему 25√3/2=12,5√3. Смотрите. Мы сокращаем в числителе и знаменателе на 2. 25:2=12,5 2:2=1. Получается, что ответы (25√3)/2+24 И 12,5√3+24 абсолютно равны. Это же тоже самое, только сокращённое, посмотрите ещё раз решение с начала, и вы убедитесь) Поэтому мой ответ верный
Этот отрезок делит четырёхугольник на 2 прямоугольных треугольника АДС и АВС.
Рассмотрим треугольник АВС.
Два катета по 6 и 8 соответсвенно.
По теореме Пифагора получаем, что гипотенуза АС= √100=10.
Площадь треугольника АВС= катет*катет/2=6*8/2=24.
Рассмотрим треугольник АДС.
Гипотенуза известна и равна 10. Катет равен 5√3.
По теореме Пифагора ищем второй катет.
Он равен= √(100-25*3)= √25=5.
Площадь треугольника АДС= 5*5√3/2=25√3/2
Площадь АВСД=площадь АВС+площадь АДС.
Площадь АВСД=(25√3)/2+24 Так. Объяснение, почему 25√3/2=12,5√3. Смотрите. Мы сокращаем в числителе и знаменателе на 2. 25:2=12,5 2:2=1. Получается, что ответы (25√3)/2+24 И 12,5√3+24 абсолютно равны. Это же тоже самое, только сокращённое, посмотрите ещё раз решение с начала, и вы убедитесь) Поэтому мой ответ верный
Приложения:
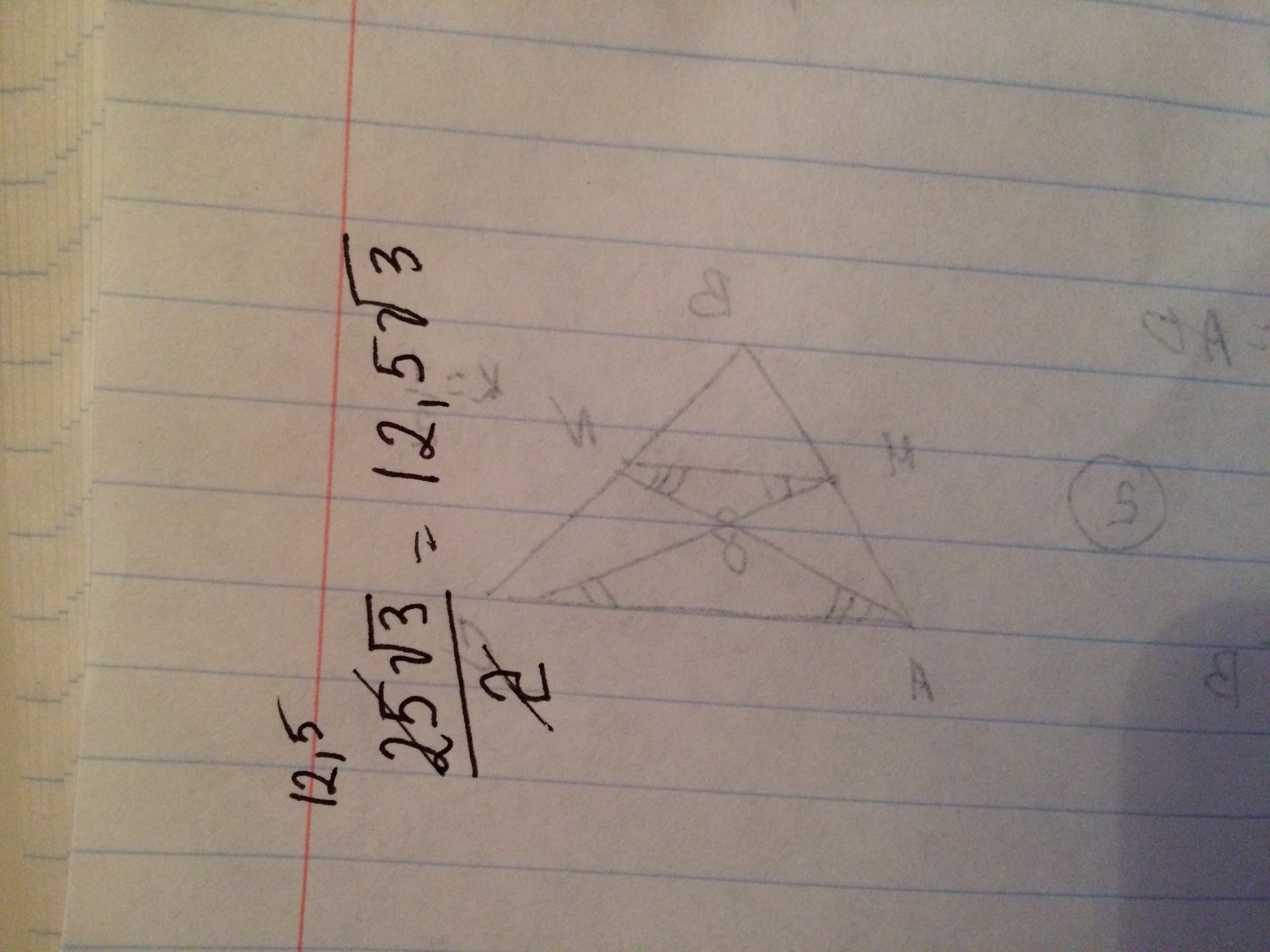
Похожие вопросы
Предмет: Алгебра,
автор: lseremeta294
Предмет: Математика,
автор: dd3820113
Предмет: Английский язык,
автор: slabkaakristina
Предмет: Українська мова,
автор: valehka101