Question

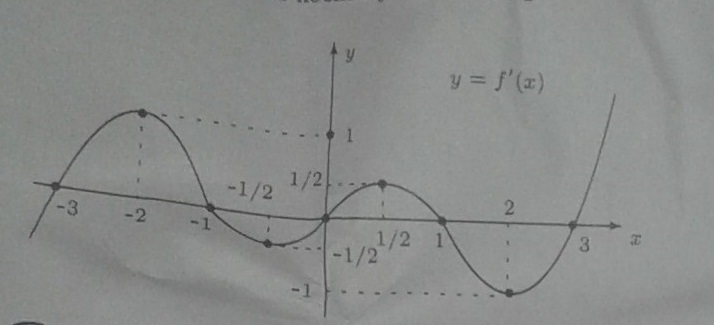
На рисунке представлен график функций y=f'(x). Вычислить 4tgα-3ctgα, где α является острым углом между касательными к графикам функций y=f(x) и y=f'(x), проведенными соответственно в точках с абсциссами x(0)=2 и x(1)= -1/2 (0 и 1 в индексе)

Answer 1

Производная равна тангенсу угла наклона касательной к графику функции в заданной точке.
Для y=f(x) в точке x(0)=2 производная по графику равна -1.
То есть: tg β1 = -1. Угол равен -45°.
Для y=f'(x) в точке x(1)= -1/2 касательная к графику производной горизонтальна, значит, угол β2 = 0°.
Тогда заданный угол α = β1 - β2 = -45° - 0° = -45°.
Тангенс угла -45° = -1, а котангенс равен 1/(-1) = -1.

Ответ: 4tgα-3ctgα = 4*(-1) - 3*(-1_ = -4 + 3 = -1.