Предмет: Геометрия,
автор: MrXgran
помогите решить. полтора часа сижу с ней, никак не идет. нужно срочно объяснить.
P.S. высота EH уходит за пределы треугольника. Поэтому и биссектриса CF пересекается с данной высотой за пределами треугольника.
Приложения:

Kulakca:
я не изменяю своим принципам и здесь )
ахха, похвально)
если будут ещё какие-нибудь вопросы, пишите мне в личную почту
а можно ее узнать, пожалуйста??
я про личку на этом сайте
аа, да, окей
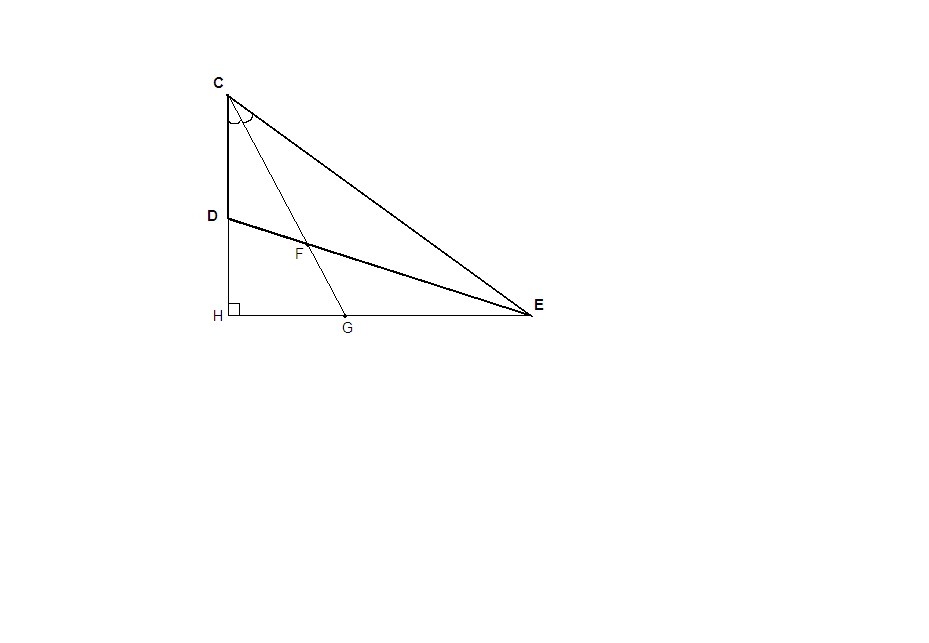
Некоторое напряжение мысли :) Ясно, что CD = EC/2; CH = (4/5)*EC; DH = EC*(4/5 - 1/2) = (3/10)*EC = (по условию) = 3/2; EC = 5; И вот тут всё становится совершенно ясным - треугольник ECH - это простейший пифагоров треугольник ("египетский") со сторонами 3,4,5 и ED и CG - биссектрисы острых углов этого треугольника. Точка F - центр вписанной окружности, точка пересечения биссектрис. Это следует из того, в каких пропорциях ED и CG делят катеты тр-ка ECH;
В прямоугольном треугольнике угол между биссектрисами острых углов всегда 135° (имеется ввиду угол, под которым из точки F видна гипотенуза). Поэтому из теоремы синусов сразу находится R = 5/(2*sin(135°)) = 5√2/2; (EC - это сторона квадрата, вписанного в такую окружность радиуса R;)
Точка F - центр вписанной окружности в треугольник ECH!!!!!! а то мало ли...
Ответы
Автор ответа:
0
По свойству биссектрисы треугольника
CD:CE = DF:FE = 2:1 ⇒ CE = 2CD
CG - биссектриса ΔCHE и по тому же свойству
CH:CE = HG:GE = 4:5
Получаем систему
CH:CE = HG:GE = 4:5
CE = 2CD
(CD + 3/2):CE = 4:5
CE = 2CD
4CE = 5CD + 15/2
CE = 2CD
8CD = 5CD + 15/2
3CD = 15/2
CD = 5/2
CE = 5
ΔCHE: cosC = CH/CE = 4/5
ΔCDE по теореме косинусов:
DE = √(25/4 + 25 - 2·5/2·5·4/5) = √(125/4 - 20) = √(45/4) = 3√5/2
Учитывая, что EF/FD = 2/1: FD = √5/2, FE = √5
cos(C/2) = √((1 +cosC)/2) = √(9/10) = 3/√10
sin(C/2) = √(1 - cos²(C/2)) = 1/√10
ΔCFE:
R = EF/(2sin∠FCE) = √5 / (2/√10) = 5√2/2
CD:CE = DF:FE = 2:1 ⇒ CE = 2CD
CG - биссектриса ΔCHE и по тому же свойству
CH:CE = HG:GE = 4:5
Получаем систему
CH:CE = HG:GE = 4:5
CE = 2CD
(CD + 3/2):CE = 4:5
CE = 2CD
4CE = 5CD + 15/2
CE = 2CD
8CD = 5CD + 15/2
3CD = 15/2
CD = 5/2
CE = 5
ΔCHE: cosC = CH/CE = 4/5
ΔCDE по теореме косинусов:
DE = √(25/4 + 25 - 2·5/2·5·4/5) = √(125/4 - 20) = √(45/4) = 3√5/2
Учитывая, что EF/FD = 2/1: FD = √5/2, FE = √5
cos(C/2) = √((1 +cosC)/2) = √(9/10) = 3/√10
sin(C/2) = √(1 - cos²(C/2)) = 1/√10
ΔCFE:
R = EF/(2sin∠FCE) = √5 / (2/√10) = 5√2/2
Приложения:
Автор ответа:
1
Я позволю себе выложить здесь оформленное решение задачи, которое дано в комментариях. Данное решение, на мой взгляд, заслуживает большего предпочтения.
Приложения:

Я не возражаю. Два момента. Надо бы пояснить, почему угол, под которым CE видна из точки F 135°. Потому что смежный с ним угол равен сумме половин острых углов прямоугольного треугольника, то есть 45°. И совсем мелочь - когда вводится новое обозначение
нужно писать "Пусть R - радиус окружности, описанной вокруг треугольника CEF"
Я думаю, задача и была составлена таким способом - взяли "египетский" треугольник, провели биссектрисы, и составили условие по получившимся значениям.
Речь идет о том, что в логической цепочке не должно быть слабых звеньев. Я как-то сдавал зачет по гидродинамике, и наш профессор (между прочим, всемирно известный ученый, и он, кажется, еще жив) ловил меня часа 4 на таких "аксиомах". Безошибочно, с хирургической точностью. Вопрос был один - "а почему?". 4 часа... а там - конформные преобразования...
Похожие вопросы
Предмет: Химия,
автор: prihodcenkoksenia58
Предмет: Биология,
автор: tymchukangelina11
Предмет: Алгебра,
автор: illiakravets9
Предмет: Английский язык,
автор: ponkrashind12
Предмет: Математика,
автор: juliya42856