Question

В правильной треугольной пирамиде апофема, равная 6 см, составляет с плоскостью основания угол 60 градусов. Вычислите площадь полной поверхности пирамиды.

Answer 1

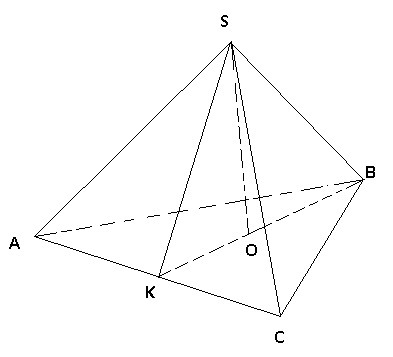
Из прямоугольного треугольника SOK: ∠OSK=90°-∠SKO=90°-60° = 30°
Против 30° противолежащий катет в 2 раза меньше за гипотенузу, т.е. $OK= \frac{SK}{2}=3\, _C_M$

OK - радиус вписанной окружности ΔАВС.
ΔАВС - правильный, значит AB=2r√3 = 2 · 3 · √3 = 6√3 см.

$S_{з ABC}= \frac{AB^2 \sqrt{3} }{4} = \frac{(6\sqrt{3})^2\cdot\sqrt{3}}{4} =27\sqrt{3}\,\, _C_M_^2$

Площадь одной грани из ΔSAC: $S_{з SAC}= \frac{AC\cdot SK}{2} = \frac{6\sqrt{3}\cdot6}{2} =18\sqrt{3}\,\, _C_M_^2$

Площадь боковой поверхности: Sбок = $3\cdot S_{з SAC}=3\cdot18\sqrt{3}=54\sqrt{3}\,\, _C_M_^2$


Найдем площадь полной поверхности

Sполн = Sосн + Sбок = $27\sqrt{3}+54\sqrt{3}=81\sqrt{3}\,\, _C_M_^2$


Ответ: $81\sqrt{3}\,\, _C_M_^2$