Предмет: Математика,
автор: Louisesa
Sin6x * cos2x< sin5x * co3x, помогите пожалуйста, хотя направление дайте как решать, очень нужно!!!!!!!
Ответы
Автор ответа:
1
sin4x+sin8x<sin2x+sin8x
sin4x-sin2x<0
2sin2xcos2x-sin2x<0
sin2x(2cos2x-1)<0
Ответ:
Приложения:
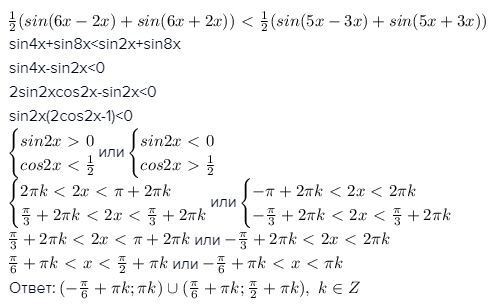
Автор ответа:
0
1/2sin(6x-2x)+1/2sin(6x+2x)<1/2sin(5x-3x)+1/2sin(5x+3x)
1/2sin4x+1/2sin8x<1/2sin2x+1/2sin8x
1/2sin4x-1/2sin2x<0
1/2*2sin2xcos2x-1/2sin2x<0
1/2sin2x(2cos2x-1)<0
1){sin2x>0⇒2πk<2x<π+2πk⇒πk<x<π/2+πk,k∈z
{cos2x<1/2⇒π/3+2πk<2x<5π/3+2πk⇒π/6+πk<x<5π/6+πk,k∈z
x∈(π/6+πk;π/2+πk,k)
2){sin2x<0⇒π+2πk<2x<2π+2πk⇒π/2+πk<x<π+πk,k∈z
{cos2x>1/2⇒-π/3+2πk<2x<π/3+2πk⇒-π/6+πk<x<π/6+πk,k∈z
x∈(-π/6+πk;πk,k∈Z)
Ответ x∈(-π/6+πk;πk,k∈Z) U (π/6+πk;π/2+πk,k)
1/2sin4x+1/2sin8x<1/2sin2x+1/2sin8x
1/2sin4x-1/2sin2x<0
1/2*2sin2xcos2x-1/2sin2x<0
1/2sin2x(2cos2x-1)<0
1){sin2x>0⇒2πk<2x<π+2πk⇒πk<x<π/2+πk,k∈z
{cos2x<1/2⇒π/3+2πk<2x<5π/3+2πk⇒π/6+πk<x<5π/6+πk,k∈z
x∈(π/6+πk;π/2+πk,k)
2){sin2x<0⇒π+2πk<2x<2π+2πk⇒π/2+πk<x<π+πk,k∈z
{cos2x>1/2⇒-π/3+2πk<2x<π/3+2πk⇒-π/6+πk<x<π/6+πk,k∈z
x∈(-π/6+πk;πk,k∈Z)
Ответ x∈(-π/6+πk;πk,k∈Z) U (π/6+πk;π/2+πk,k)
Похожие вопросы
Предмет: Оʻzbek tili,
автор: Аноним
Предмет: Химия,
автор: olesiaostapiyk
Предмет: Английский язык,
автор: lesavasilina1986
Предмет: Геометрия,
автор: Romiros22
Предмет: Алгебра,
автор: katkatrap