Предмет: Математика,
автор: timuriosan
Решите пожалуйста неравенство . Пожаалуйста)
Приложения:
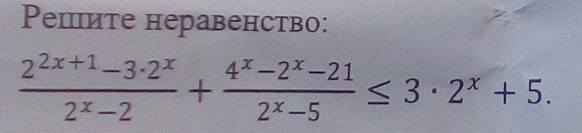
LyubaAlexandorovna:
Можно по действиям?
Да, подробнее желательно(( с решением
Ответы
Автор ответа:
1
ОДЗ 2^(x)-2≠0, х≠1, 2^(x)-5≠0, х≠loq2(5)
Числитель первой дроби:(для каждого выражения применяю замену 2^x=t)
2^(2*х+1)-3*2^(x)=2*2^(2*x)-3*2^(x)=2*t²-3*t
Знаменатель первой дроби:
2^x-2=t-2
Числитель второй дроби:
4^(x)-2^(x)-21=2^(2*x)-2^(x)-21=t²-t-21
Знаменатель второй дроби:
2^(x)-5=t-5
Запишем сумму:
(2*t²-3*t)/(t-2)+(t²-t-21)/(t-5)=
Приведём к общему знаменателю (t-2)*(t-5)=t²-7*t+10
Запишем числитель
(2*t²-3*t)*(t-5)+(t²-t-21)*(t-2)=3*t³-16*t²-4*t+42
Запишем полученное выражение:
(3*t³-16*t²-4*t+42)/(t²-7*t+10)-(3*t+5)≤0
Уможим обе части неравенства на t²-7*t+10
3*t³-16*t²-4*t+42-3*t³+16*t²+5*t-50≤0
t-8≤0
t≤8
2^(x)≤8
2^(x)≤2³
Так как 2>1, равны основания, равенство для степеней сохраняется.
х≤3
C учётом ОДЗ х∈(-бесконечность;1)+(1; ㏒2(5)+(㏒2(5); 3]
Числитель первой дроби:(для каждого выражения применяю замену 2^x=t)
2^(2*х+1)-3*2^(x)=2*2^(2*x)-3*2^(x)=2*t²-3*t
Знаменатель первой дроби:
2^x-2=t-2
Числитель второй дроби:
4^(x)-2^(x)-21=2^(2*x)-2^(x)-21=t²-t-21
Знаменатель второй дроби:
2^(x)-5=t-5
Запишем сумму:
(2*t²-3*t)/(t-2)+(t²-t-21)/(t-5)=
Приведём к общему знаменателю (t-2)*(t-5)=t²-7*t+10
Запишем числитель
(2*t²-3*t)*(t-5)+(t²-t-21)*(t-2)=3*t³-16*t²-4*t+42
Запишем полученное выражение:
(3*t³-16*t²-4*t+42)/(t²-7*t+10)-(3*t+5)≤0
Уможим обе части неравенства на t²-7*t+10
3*t³-16*t²-4*t+42-3*t³+16*t²+5*t-50≤0
t-8≤0
t≤8
2^(x)≤8
2^(x)≤2³
Так как 2>1, равны основания, равенство для степеней сохраняется.
х≤3
C учётом ОДЗ х∈(-бесконечность;1)+(1; ㏒2(5)+(㏒2(5); 3]
Похожие вопросы
Предмет: Биология,
автор: miha23763
Предмет: Литература,
автор: bgklimlim
Предмет: Українська мова,
автор: krusa8284
Предмет: Окружающий мир,
автор: 1agam
Предмет: Алгебра,
автор: Аноним