Question

Помогите с выш матом.

1. Исследовать на экстремум функцию: x^2+4*y^2+2*xy-4*x+8*y+1.

2. Вычислить площадь фигуры, ограниченной линиями:
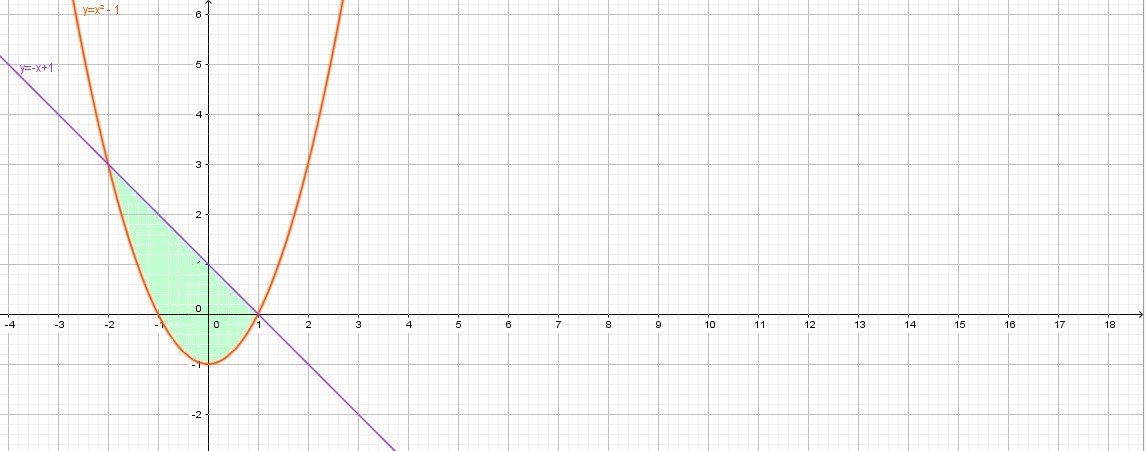
y=x^2-1, y=-x+1

Answer 1

1. Найдем частные производные 
$\displaystyle \left \{ {{ \frac{\partial z}{\partial x} =2x+2y-4=0} \atop {\frac{\partial z}{\partial y} = 8y+2x+8=0}} \right.$

Решив систему уравнений, получим

$\displaystyle \left \{ {{x=4} \atop {y=-2}} \right.$

Найдем частные производные второго порядка

$\displaystyle \frac{\partial^2 z}{\partial x\partial y}=2;\,\,\,\,\,\,\,\,\,\, \frac{\partial^2z}{\partial x^2} =2;\,\,\,\,\,\,\,\,\,\,\, \frac{\partial^2 z}{\partial y^2} =8.$

Составим матрицу   $\left(\begin{array}{ccc}2&2\\ 2&8\end{array}\right)$

$a_{11}=2\ \textgreater \ 0\\ a_{22}= \left|\begin{array}{ccc}2&2\\2&8\end{array}\right|=2\cdot8-2\cdot2\ \textgreater \ 0$

По критерию Сильвестра, точка M(4;-2) - точка минимума


Задание 2. 
$y=x^2-1$ графиком функции является парабола, ветви направлены вверх.
$y=-x+1$ - прямая, проходящая через точки (0;1), (1;0)

Поскольку график функции y=-x+1 расположен выше чем график функции $y=x^2-1$, то площадь фигуры будем искать следующим образом

$\displaystyle \int\limits^1_{-2} {(-x+1-(x^2-1))} \, dx =\int\limits^1_{-2} {(-x^2-x+2)} \, dx =\\ \\ \\ =\bigg(- \frac{x^3}{3}- \frac{x^2}{2}+2x\bigg)\bigg|^1_{-2} =-\frac{1}{3}-\frac{1}{2}+2-\frac{8}{3}+2+4=4.5$