Предмет: Алгебра,
автор: Дарья11111111
Помогите решить уравнение
Приложения:
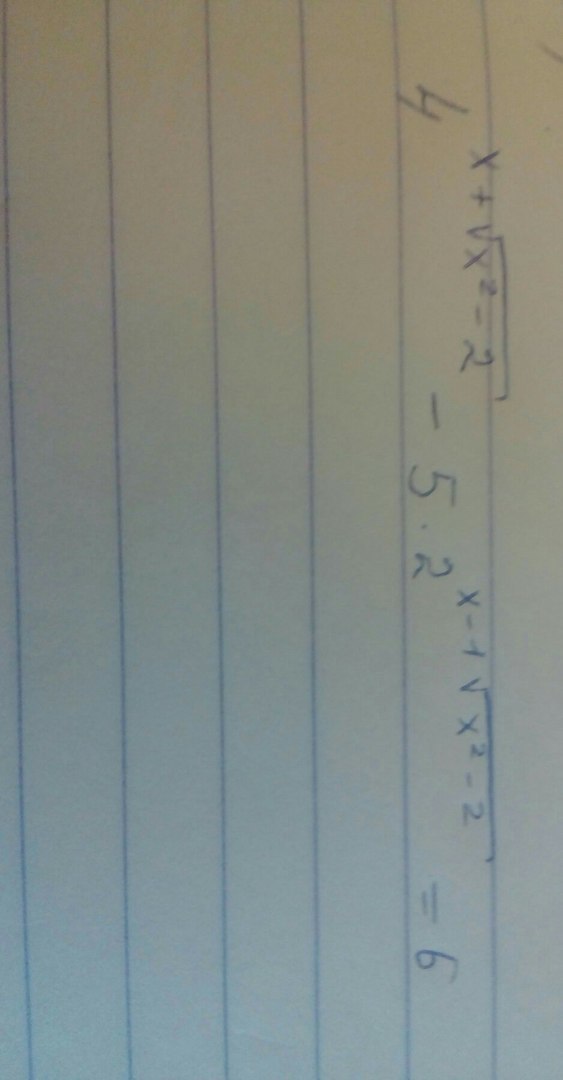
park01:
в выражении степени двойки нписано (x-1)*(x^2-2)^(1/2)?
Ответы
Автор ответа:
1
4^(x+√(x²-2))) - 5*2^(x-1+√(x²-2)) = 6
одз x²>=2 x∈(-∞ -√2] U [√2 +∞)
2^2(x+√(x²-2))) - 5*2^(x+√(x²-2))/2 = 6
2^(x+√(x²-2)) = t t>0
t² - 5/2*t = 6
2t² - 5t - 12 =0
D=25+4*12*2 = 121 = 11²
t₁₂=(5+-11)/4 = 4 -3/2
1. 2^( x+√(x²-2)) = 4
2^( x+√(x²-2)) = 2^2
x+√(x²-2) = 2
√(x²-2) = 2 - x (x<=2 корень квадратный больше равен 0)
x²-2 = 4 - 4x + x²
4x=6
x=6/4=3/2
√2 < 3/2 < 2 да корень
2. 2^(x+√(x²-2)) = -3/2
Решений нет 2^(x+√(x²-2)) >0
Ответ 3/2
одз x²>=2 x∈(-∞ -√2] U [√2 +∞)
2^2(x+√(x²-2))) - 5*2^(x+√(x²-2))/2 = 6
2^(x+√(x²-2)) = t t>0
t² - 5/2*t = 6
2t² - 5t - 12 =0
D=25+4*12*2 = 121 = 11²
t₁₂=(5+-11)/4 = 4 -3/2
1. 2^( x+√(x²-2)) = 4
2^( x+√(x²-2)) = 2^2
x+√(x²-2) = 2
√(x²-2) = 2 - x (x<=2 корень квадратный больше равен 0)
x²-2 = 4 - 4x + x²
4x=6
x=6/4=3/2
√2 < 3/2 < 2 да корень
2. 2^(x+√(x²-2)) = -3/2
Решений нет 2^(x+√(x²-2)) >0
Ответ 3/2
а как из х-1 получилось х+1
2^-1 превратилось в 1/2 ///// 2^(x-1)=2^x/2
Спасибо)
Автор ответа:
0
делаем замену:
x+sqrt(x^2-2)=y
получим:
4^y-5*2^(y-1)=6
2^2y-5*(1/2)*2^y=6
делаем еще одну замену:
2^y=t
получим:
t^2-2,5t-6=0
2t^2-5t-12=0
D=25+96=121
t1=(5+11)/4=4
t2=-6/4=-1,5
2^y=-1,5
y - нет корней
2^y=4
2^y=2^2
y=2
x+sqrt(x^2-2)=2
2-x=sqrt(x^2-2)
возводим обе части в квадрат, но:
2-x>=0; x<=2
x^2-2>=0
4-4x+x^2=x^2-2
-4x=-6
4x=6
x=6/4=1,5
проверяем:
1,5<=2
1,5^2-2>=0; 0,25>=0
верно, значит 1,5 является корнем уравнения
Ответ: x=1,5
x+sqrt(x^2-2)=y
получим:
4^y-5*2^(y-1)=6
2^2y-5*(1/2)*2^y=6
делаем еще одну замену:
2^y=t
получим:
t^2-2,5t-6=0
2t^2-5t-12=0
D=25+96=121
t1=(5+11)/4=4
t2=-6/4=-1,5
2^y=-1,5
y - нет корней
2^y=4
2^y=2^2
y=2
x+sqrt(x^2-2)=2
2-x=sqrt(x^2-2)
возводим обе части в квадрат, но:
2-x>=0; x<=2
x^2-2>=0
4-4x+x^2=x^2-2
-4x=-6
4x=6
x=6/4=1,5
проверяем:
1,5<=2
1,5^2-2>=0; 0,25>=0
верно, значит 1,5 является корнем уравнения
Ответ: x=1,5
Похожие вопросы
Предмет: Українська мова,
автор: sodjdjid
Предмет: Физика,
автор: skorisenkoivan83
Предмет: Английский язык,
автор: akbelle12
Предмет: Русский язык,
автор: Аноним